「気泡を含む液体中を伝わる圧力波」

東京農工大学工学部機械システム工学科　亀田正治

１．はじめに

　本稿では，気泡の存在が圧力波に与える影響を，基礎的な事項を中心に解説する．より深く知りたい場合は，詳しい専門書[1][2]にあたることを薦めたい．
　流体現象は，流れ (flow) と波 (wave) に大きく分けられる．波は，流体を介して，ある変動が伝わっていく現象をさす．圧力波は，流体中に見られる波の一形態であり，音波 (sound wave)，衝撃波 (shock wave) などに分類される．
　気泡の存在は，流れ現象を複雑にする．この状況は圧力波についても同様である．

図１　気泡の膨張・収縮運動にともなって音が発生する

　

図２　液滴の突入にともなって発生する気泡と音

　圧力波の場合，複雑さを生むポイントは，液体中の気泡が，それ自身の運動，特に，膨張・収縮（体積）運動によって音を発生することにある（図１）．例えば，雨が川や海に降り注ぐとき，水中に置いたマイクロフォンでとらえた音は，特有の周波数成分（約14 kHz）を持つことが知られている[3]．これは，図２[4]に示すように，雨滴の突入に付随して貫入した気体が取り残されることによって生じた気泡の膨張・収縮によるものである．

　

２．圧力変動にともなう気泡の膨張・収縮運動

　図３のように，液体中に気泡を含んだ領域 (bubble layer) がある状況を想定しよう．左側に置かれた発振器から出た音波が右に伝わり，気泡群に到達したとき，音波はどうなるであろうか？　音の伝わり方で注目されるのは，まず，図の中にあるように，反射 (reflection)と透過 (transmission) であろう．また，その際の音圧の変化も気になるであろう．

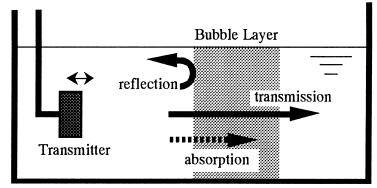
図３　気泡群による音の反射，透過，吸収

　図４は，線形理論[5]に基づいて，気泡を含む液体中を伝わる音波の性質（音響特性）を表したグラフである．音の周波数fを横軸としたときの，音速 (位相速度, phase velocity)，および，透過率 (transmittance) を示している．音速や透過率が，周波数によって大きく変化することがわかる．

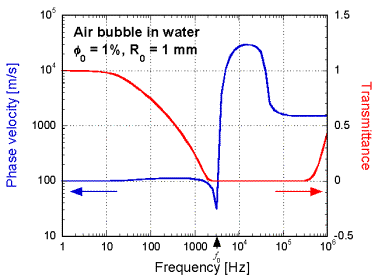
図４　気泡を含む液体の音響特性

　波の伝わる特性（音速など）が周波数によって変化する性質を，「分散性」(dispersion) という．気泡を含む液体が分散性を有するのは，はじめに述べたとおり，気泡の膨張・収縮運動と密接な関係がある．

次の式は，気泡半径の時間変化R(t) を表す基本的な式（Rayleighの式）である．

・・・ (1)

ただし，は液体の密度を， は気泡表面における液体圧力を， は気泡から十分遠方の液体圧力をそれぞれ表す．気泡表面の液体圧力は気泡内気体の圧力とほぼ等しいから，式(1)は，気泡の半径変化が気泡内外の圧力差によって生じる，ということを意味している．

微小な半径変化に対しては，式(1)を線形化した次式を用いる．

位相速度，透過率ともに周波数依存性がある

・・・ (2)

ただし ，であり，，はそれぞれ，静止状態における気泡半径，液体圧力を表す．式(1)は，単振動を表す式であり，β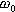， はそれぞれ，減衰定数 (damping constant)，固有角振動数 (natural angular frequency) を意味する．

　固有振動数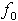は，

・・・ (3)

で表される．κ は気泡内気体のポリトロープ指数（断熱変化ならκ＝γ (比熱比), 等温変化ならκ＝1），α は気液間に働く表面張力係数である．固有振動数は平衡半径R0にほぼ反比例する．例えば，水中の空気気泡の場合， = 1 mmのとき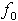は 約3kHzになる．一方，β は，液体の粘性，圧縮性，気液間の熱交換に依存する値である(6)．

　単振動である以上，周囲液体の圧力変化 に応じて，気泡半径の変動の様子は変化する．例えば，圧力変化が正弦的に与えられるとすると，半径変動の振幅は周波数に依存する．さらに，その周波数f が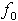より小さい場合は，周囲圧力の上昇にともなって気泡サイズは小さくなり，f が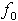 より大きい場合は，逆に，圧力上昇にともなって気泡サイズは大きくなる．

　

３．気泡を含む液体中を伝わる音の性質

　気泡は，周囲液体の圧力変化に対してパッシブに応答する音源であり，その性質は，気泡のサイズや圧力変化の周波数などによって大きく変化する．

　ここで，図４をもう一度詳しく見直してみよう．グラフは，体積割合（ボイド率）にして1％の空気を半径1 mmの気泡として分散させた気液混合物（圧力は100 kPa）の音響特性を表したものである．3kHz付近を境に，音速，透過率ともに大きく変化していることに気づくだろう．これは，固有振動数を境に，気泡の半径変化の位相が反転するためである．

（１）f <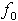の場合

　3kHz以下の周波数では，音速が100m/s程度になっている．この値は，水の音速1500m/sはもとより，常温の空気中を伝わる音の速さ340m/sよりもはるかに小さい．

音速aは，

・・・ (4)

から求まる．固有振動数より低い周波数の場合，液体圧力の上昇にともなって気泡は縮む，すなわち，気液混合物の密度は増加する．気泡の体積変化にともなう気液混合物密度の変動は大きいから，式(4)に従って，音速を単位圧力変化量に対する気液混合物の密度変化という眼で見れば，気液混合物の音速は，気体のみ，あるいは，液体のみの場合に比べて小さくなるわけである．

　理論的には，低周波数領域において，

・・・ (5)

が成り立つ．ここで，φ はボイド率を表し， ， はそれぞれ，液体，気体単相の音速を表す．また，ボイド率が0.1%以上であれば，式(5)は近似的に，

・・・ (6)

式(5), (6)は，気泡の膨張・収縮にともなう気体の状態変化を等温変化と考え，かつ，気泡はいつも液体と同じ並進速度で動く（スリップなし）と仮定して得られており，「等温平衡音速」と呼ばれている．

図５は，式(5)によって描いた音速のボイド率依存性である．ただし， 100 kPa, 1000K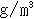とした．φ < 0.5の範囲では，ボイド率が高くなるにつれて音速は低下する．φ = 0.5のときaは最小値20 m/s（72 km/h）となる．

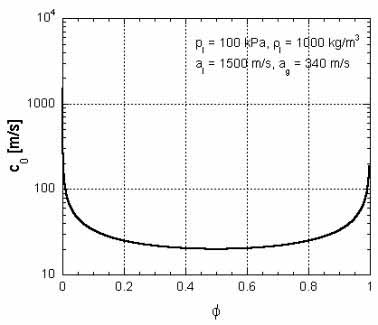
図５　等温平衡音速

図６　平行平板間を伝わる衝撃波と圧力波形
平板中央部にのみ気泡がある（ボイド率0.4%）．波面が湾曲し，中央部に高圧スポットができることがわかる

　音速のボイド率依存性は，液体の一部に気泡が集まっている場合，すなわち，ボイド率の空間不均一が存在する状況下で，顕著な影響をおよぼす．

　図６は，平行平板間を伝わる衝撃波の数値計算結果[7],[8]である．左から右に向かって正の圧力ステップが伝わっていく．気泡は平板間の中心付近にのみ存在している．気泡が集積している部分の音速は，周囲に比べて小さくなるため，圧力波の波面が中心に向かって湾曲している．気泡群が凸レンズの役目を果たし，中心部に圧力が集まってくる．この結果，中心部に高圧のスポットが形成される．

　液体中に気泡が不均一に存在している状況下での圧力の伝わり方は，キャビテーション気泡群の崩壊圧力を決める重要なファクターである．その点に着目した解析が進められている[9]．

（２）f > 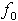の場合

　再び，図４に注目しよう．3kHzから数10kHzに目を向けると，音速が毎秒1万mにも達していることに気づく．しかし，これは見かけの値に過ぎない．透過率に見ればわかるとおり，この領域の音の透過率はほぼゼロ，つまり，音は伝わらない．

図７　円管内に等間隔に置かれた気泡群を伝わる圧力波伝播シミュレーション（概略図）

　この現象は，波のカットオフと呼ばれている．図７，８をもとに，そのメカニズムを説明しよう．図７，８は，細い円管内に気泡を並べた液体中を伝わる圧力の様子を，直接数値計算によって調べたものである[10]．計算条件は図７にあるとおりである．初期気泡半径を0.5mmとしたので，気泡の固有振動数は約6kHzである．

　図８は，f = 14kHzに対する計算結果である．(a)を見ると，左端で強制的に圧力変動を与えているにもかかわらず，その変動はまったく右側に伝わっていない．

<Click>
図８　気泡の固有振動数より少し高い周波数を持つ正弦波の伝播挙動
液体に加えられた圧力変動が，気泡周囲に作り出される逆位相の圧力変動によって打ち消される

　液体の圧力変化が気泡の固有振動数を上回っている場合，液体の圧力上昇にともなって，気泡半径が増加，すなわち気泡内気体の圧力は低下する．図８(b)を見ると分かるように，気泡内圧力と液体圧力の位相はほぼ反転している．さらに，図８(c)に示す気泡周りの圧力場に着目すると，気泡周囲の圧力は気体圧力と一致する方向に変化していることがわかる．そのため，気泡によって生じる圧力低下量が，液体の圧力上昇と同程度であれば，液体側の圧力変動は打ち消される．なお，自動車騒音の低減技術の一つに，スピーカーを使って逆位相の音を加える方法があるが，音が打ち消されるメカニズムは図８と同様である．

４．おわりに

　気泡と圧力変動との関係は，キャビテーション，水中音響，ソノケミストリーなど，多岐にわたっている．筆者は最近，火山学の研究者と共同で，火山噴火のメカニズムに対する気泡運動の影響を解明する仕事にも取り組んでいる[11]．いずれの分野も未だに分かっていないことは数多く残されている．さらに多くの人たちが，この研究分野に関心を持ち，現象解明に取り組んでくれることを願っている．

　

参考文献

[1]日本流体力学会編，「流体における波動」（朝倉書店，1989）.
[2]Leighton, T.G., The Acoustic Bubble (Academic Press, 1994).
[3]Pumphrey, H.C. and Elmore, P.A., "The entrainment of bubbles by drop impacts," J. Fluid Mech. 220 (1990), 539.
[4]Prosperetti, A. and Oguz, H.N., "The impact of drops on liquid surfaces and the underwater noise of rain," Annu. Rev. Fluid Mech. 25 (1993), 577.
[5]Commander, K.W. and Prosperetti, A., "Linear pressure waves in bubbly liquids: Comparison between theory and experiments," J. Acoust. Soc. Am. 85 (1989), 732.
[6]Prosperetti, A. "The thermal behaviour of oscillating gas bubbles," J. Fluid Mech. 222 (1991), 587.
[7]亀田正治・松本洋一郎, "気泡流中における衝撃波の伝播 (第3報)," 日本機械学会論文集 61-584 B (1995), 1238.
[8]Kameda, M. and Matsumoto, Y., "Shock waves in a liquid containing small gas bubbles," Phys. Fluids 8 (1996), 322.
[9]島田正仁・松本洋一郎・小林孝, "クラウドキャビテーションの動力学とキャビテーションエロージョン," 日本機械学会論文集 65-634 B (1999), 1934.
[10]沼田規好・亀田正治, "気泡を含む液体中を伝わる圧力波の直接数値解析," 日本機械学会流体工学部門講演会講演論文集 (1998), 131.
[11]市原美恵・亀田正治, "火山噴火を解き明かす -室内実験の試み," 可視化情報学会誌 22 (2002), 223.