2.数値計算
2.1 支配方程式
ネマティック液晶の流動を記述する完成度の高い理論としてLeslie-Ericksen(L-E)理論[2]〜[4]を構成方程式として用いる.L-E理論では,偏差応力テンソルτ は次式で表される.
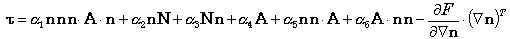 ------ (1) ------ (1)
ここで は液晶分子の局所的平均配向方向を表す単位ベクトルで,ディレクタと呼ばれる.広義の意味でディレクタの向きと分子の配向方向は同一である. はレズリー粘性係数,A
は変形速度テンソル,N はディレクタの相対角速度ベクトル,F はディレクタの空間的弾性ひずみに基づく自由エネルギ密度で はレズリー粘性係数,A
は変形速度テンソル,N はディレクタの相対角速度ベクトル,F はディレクタの空間的弾性ひずみに基づく自由エネルギ密度で
 ------ (2) ------ (2)
と記述される.ここでK1 ,K2 ,K3 は,それぞれディレクタの空間的広がり,ねじれ,曲がりに関する弾性定数である[5].式(1)を,外力Fを付加した運動方程式に代入し,連続の式と連立させて数値解を求めるが,等方性流体と異なり分子の配向方向であるディレクタ
n を規定する必要がある.そこで角運動方程式
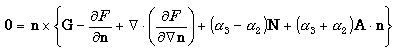 ------ (3) ------ (3)
を用いる. n×G は外場がディレクタに及ぼす単位体積当たりのトルクである. FおよびGは,例えば外場として磁場Hを選択すれば,
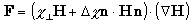 ------ (4) ------ (4)
 ------ (5) ------ (5)
と表される.ただ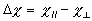 は磁化率の異方性, は磁化率の異方性, および および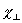 はそれぞれディレクタに平行,および垂直方向の反磁性磁化率である.外場として電場を選択すれば, はそれぞれディレクタに平行,および垂直方向の反磁性磁化率である.外場として電場を選択すれば,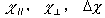 を誘電率に置換すればよい. を誘電率に置換すればよい.
2.2 計算結果
図1に,平行平板間の静止状態にあるネマティック液晶PAA(p-azoxy-anisole)[6]に,一様磁場を印加した場合に誘起される速度(背流)
w の時間変化を示す.横軸 y は平板間の位置座標である.平板間隔を1mm,下壁面の配向角に対する上壁面の配向角
θw を−30°に設定した.図のように静止状態からスタートし,平板間の下半分では正の,上半分では負の速度が発生している.一連の変化はおよそ5秒間で生じており,
t =3 sまでは増速,その後は粘性のため減速に転じている.また,最大で概略0.04mm/s程度の速度が誘起されている.

(図1) 速度分布の時間変化
図2に,磁場の印加により誘起される最大速度と上壁面の配向角θw の関係を示す.図よりθw =
0°の場合,背流の分布は平板間中央面( y = 0.5 mm)に関して反対称になっている.従って局所的には有限の速度が発生するが,平板間全体にわたる流量は0である.
θw を減少(絶対値を増加)させると反対称分布は崩れ,その結果流量も有限値をとる.図示はしていないが,θw =−180°のとき,背流は完全な一方向分布となる.

(図2) 速度分布に及ぼす上壁面の配向角θwの影響
3.流動実験
上述した背流の発生を実験的に追認するため,ネマティック液晶を封入した間隔50μmのガラス平板間に直流電圧10
Vを印加して顕微鏡観察を行った. θw =−90°である.本研究では,物性値を入手しやすい理由から数値計算では外場として磁場を選択したが,実験ではその容易さから電場を選択した.液晶流動に及ぼす電場と磁場の差異はなく,上述したように磁化率を誘電率に置換するのみである.液晶の流動を可視化するため,直径約2.5μmのポリスチレン粒子を液晶に適量混入した.図3(a),(b)は,それぞれ電圧印加前と印加後0.3
s時における平板間の中央位置での顕微鏡画像である.図より粒子が移動しており,電場による配向の変化に伴って流動の発生が確認された.画像解析により,速度の大きさは5.3μm
/0.2 sであった.

(a) 電場印加前

(b) 電場印加後
図3 液晶中における微粒子の移動の顕微鏡観察
4.おわりに
以上のように液晶に電場または磁場を印加することで流動が発生することを数値的,且つ実験的に確認した.この結果を応用すれば極小サイズ(本研究は連続体力学に基づいていることから,代表長さが数10
nm〜100 nm以上について成立する)の様々なアクチュエータを開発できる.例えば平行平板の一方が固定され,他方が平面方向に可動であれば,電圧印加により平板を運動させること,またその精密制御も可能となる.また液晶が異方性"液体"であることを考えれば,どのような形状のデバイスにも適合できる.すなわち,上述の平板を曲板に置き換えることもでき,さらには二重円筒間に液晶を充填すればモータの開発にもつながる[7].ここで言及したアクチュエータはほんの数例に過ぎず,今後,液晶のメカニクス・ダイナミクスに関する幅広い研究が待たれる.
参考文献
[1] 例えば,Chandrasekhar,
S.:液晶の物理学,1995,吉岡書店.
[2] Ericksen, J. L.:Arch. Ration. Mech. Anal., 4 (1960), 231.
[3] Ericksen, J. L.:Trans. Soc. Rheol., 5 (1961), 23.
[4] Leslie, F. M.:Arch. Ration. Mech. Anal., 28 (1968), 265.
[5] Frank, F. C.:Discuss. Faraday Soc., 25 (1958), 19.
[6] Tseng, H. C., ほか2名:Phys. Fluids, 15 (1972), 1213.
[7] 特開2003−113814.
|