１．はじめに
現在，大型タンカーなどの船舶が水から受ける抵抗は，その大部分が摩擦抵抗であるため，摩擦抵抗の低減はそのまま船舶の輸送効率の向上へとつながる．しかしながら，従来までのLEBU
(Large-Eddy Break-Up device)などの抵抗低減デバイスでは高い軽減率は望めず，また生物付着による汚損などの問題が生じるため適用が困難である．このため，最近では，マイクロバブル（微小気泡）を乱流境界層に吹き込むことによって摩擦抵抗を低減させるという技術に注目が集まっている[1-2]．しかしながら，現在までのところ，この技術による摩擦抵抗低減メカニズムの包括的な実験的解明はなされていない．本稿では，画像処理によるマイクロバブル流の乱流変調計測で得られたデータを紹介する．
２．PTV/LIFによる液相計測
２．１．実験装置および実験方法
図１に本研究で用いた実験装置の概略図を示す．チャネルは，透明アクリル樹脂製で，平板間幅2hが15 mm，奥行きが100
mm，全長が3000 mmである．作動流体は，フィルタにより濾過された水であり，タンク，ポンプ，電磁流量計を介して回流する．気泡は，チャネル上流の縮流部から1028
mm下流位置において，チャネル上部に設置された気泡発生装置から，コンプレッサーを用いて注入される．座標軸は，流れ方向をx（x
= 0：気泡注入部），鉛直方向をy（y = 0：チャネル上壁面），奥行き方向をz（z = 0：チャネル中心）とする．計測部は，x
= 500 mm，z = -30 mmの位置に設定した．
本研究では，液相場の計測手法として時系列多点同時計測が可能なPTV (Particle Tracking Velocimetry)を用いる[3]．さらに，従来の混相乱流計測において問題視されてきた気泡界面での散乱光や容器壁でのハレーション等の光学的問題を解決するために，LIF
(Laser Induced Fluorescence)を併用する．トレーサ粒子には，比重約1.03，粒子径1〜数十
mmの蛍光発光粒子を用いた．蛍光粒子の吸収波長帯は，約460〜550 nmであり，蛍光発光の波長帯は，約550〜700
nmである．PTVの励起光源は，Nd:YAGレーザ(ニューウェーブリサーチ：25 mJ, λ = 532
nm)である．PTV/LIFでは，粒子の蛍光発光のみの撮影が必要であるため，カットオフフィルタ用いてレーザ光を遮断する．レーザとCCD
カメラとの同期は，パルスジェネレータを介して行われる．
図１ 実験装置概略図
２．２．実験結果および考察
1条件あたり約1000ペアの蛍光粒子画像を用いることにより，液相場の平均速度分布，乱れ度分布，レイノルズ応力分布を算出した．格子分割数は24点であり，これにより1格子間隔は，約0.297
mmとなる．
図２−４に，液体平均流速 Um =
5 m/s，Um とチャネル半幅h
に基づくレイノルズ数 Rem
= 28600の条件での液相場の平均流速分布，乱れ度分布，レイノルズ応力を示す．図２中の記号は，流れ方向および鉛直方向の液相平均速度であり，図３中のそれは，流れ方向および鉛直方向の液相乱れ度である．図３および４の縦軸は，摩擦速度 Uτ および 
によって正規化されている．なお，図中のボイド率α
は，液体流量Qw と空気流量QG を用いて，α=
QG /
( QG +Qw )として定義される．図２より，ボイド率の増加ともに，壁面近傍の液相速度が僅かに低下することが判る．一方，図３より，ボイド率の増加とともに，流れ方向および鉛直方向の乱れ度が増加することが判る．これは，気泡が誘起する擬似乱れに起因すると考えられる．さらに，図４より，ボイド率の増加とともに，レイノルズ応力が低下することが判る．これは，個々の気泡運動により，液相速度変動の相関が低下したためであろう．
図２ 液相平均流速分布
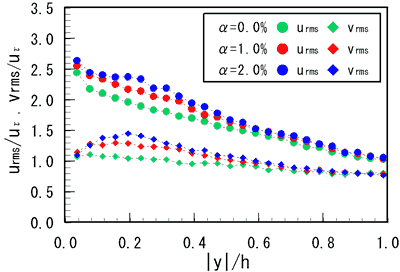
図３ 液相乱れ度分布
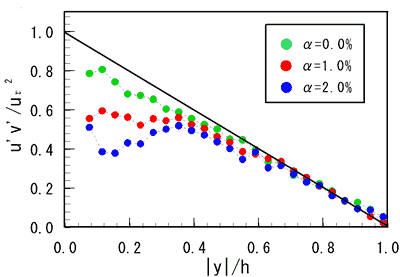
図４ 液相レイノルズ応力分布
３．PTV/LIF/ISTによる液相場と気泡群の同時計測
３．１．同時計測システム
混相乱流場の乱流変調は，液相場と気泡群との局所相互干渉に強く依存している．このため，乱流変調機構を解明するには，液相場と気泡群運動とを同時に計測する必要がある．そこで，本節では，PTV/LIF/ISTを用いた液相場と気泡群との同時計測システムを提案する．ここで，IST
(Infrared Shadow Technique)とは，赤外線によるバックライト法によって気泡像を得る手法である[4]．
実験装置の概要は，2･1節と同じである．図５は，撮影部の拡大図であり，流路のある断面部分を示す．本計測システムでは，PTVとISTを行うために2台のCCDカメラが用いられる．図中の水平方向のカメラはPTV/LIF用，鉛直方向のカメラはIST用である．PTV/LIFの励起光源は，YAGレーザ(
λ = 532 nm )であり，ISTの光源は，赤外線LED群( λ= 850 nm )である．計測部は，x
= 500 mm，z = 0 mmの位置であり，この領域に照射された光は，それぞれ，約10 mm離れたミラーを介して上向きに反射する．可視光線と赤外線との分離には，可視光を反射し，赤外線を透過させるコールドミラーが用いられる．さらに，PTV/LIFでは，粒子の蛍光発光のみの撮影が必要であるため，カットオフフィルタ用いてレーザ光を遮断する．
図５ PTV/LIF/ISTシステム
３．２．実験結果および考察
図６に，α = 0.5, 1.0 %の条件における計測結果を示す．図中の赤矢印は，PTV/LIFによって得られた液相速度ベクトルであり，白い領域は，ISTにより得られた気泡投影図である．画像上部は，チャネル上壁面に相当する．気泡速度ベクトルは，原画像においてピントのあった気泡のみから算出した．図から，気泡近傍の液相速度ベクトルおよび気泡速度ベクトルが良好に取得されていることが確認できる．このことから，本計測システムによって，液相場と気泡群との同時計測が十分に可能であると言える．今後は，マイクロバブルによる摩擦抵抗低減メカニズムを明らかにするために，乱流場と気泡群運動との局所的相互干渉を明らかにする予定である．
(a) α
= 0.5 %
(b) α
= 1.0 %
図６ 計測結果 (Um =
5 m/s, Rem= 38000)
４．おわりに
マイクロバブル流のように非常に多くの気泡を含んだ流れ場に対して計測を行う場合，気相と液相の速度を明確に分離する事が難しく，両相の速度情報が混同しがちになる．このことは，画像処理計測に限らず，熱線流速計やLDV等の一般の流体計測に対しても同様である．この問題を解決するには，計測された速度の結果のみからこれらの判別をするのではなく，計測法の基本原理に立ち返り，適切なデータ処理をすることが必要である．著者らは，画像処理技術を駆使し，気泡流乱流の微細構造の詳細を明らかにしようとしているが，現在までのところ，問題点も数多く残されている．ここに紹介した同時計測システムを用い，得られた画像から気液両相の情報を的確に弁別する方法を確立することによって抵抗低減メカニズム解明の糸口をつかみかけており，今後の展開が期待されている．
参考文献
[1]Madavan, N.K., Deutsch, S., Merkle, C.L., Reduction
of turbulent skin friction by microbubbles, Phys. Fluids
(1984), 27, 356-363.
[2]Kodama, Y., Kakugawa, A., Takahashi, T., Kawashima,
H., Experimental study on microbubbles and their applicability
to ships for skin friction reduction, Int. J. Heat and
Fluid Flow (2000), 21, 582-588.
[3]Ishikawa, M., Murai, Y., Wada, A., Iguchi, M., Okamoto,
K., Yamamoto, F., Novel algorithm for particle tracking
velovimetry using the velocity gradient tensor, Experiments
in Fluids (2000), 29-6, 519-531.
[4]藤原暁子･菱田公一, 管内気液二相流の微細乱流構造, 日本機械学会論文集Ｂ編, 68-668 (2002),
1143-1150.
