東京都の新型コロナウイルス感染症流行に関する解析と抑圧対策について
小野京右,菊地勝昭
1.まえがき
新型コロナウイルス(COVID-19)の強襲により人類が,世界が,そして日本が歴史的な試練に陥っている.日本は早期の自粛要請により感染爆発を免れた.約一ケ月半の3密に係る社会・経済活動の自粛により3月半ば以前の状態に収束し,6月以降,社会・経済活動の再開が段階的に進められている.しかしなお7月下旬現在,60%前後の感染経路不明者が報告され,第2波の懸念が人々を支配している.
筆者らは感染症流行に関しては素人であるが,自然現象の解析により技術進歩に寄与してきた専門家として,感染症対策も感染症流行現象に対する数理解析により必然的に得られるとの信念から,東京都の新型コロナの流行状況に対する分析を行ってきた.小野は自粛による感染率と検査・隔離率の感染者数に及ぼす基本的な数理モデルから,感染症流行に関するSIR理論(1)の最も基本的な式を導出し,感染率の低下と同様に検査・隔離の強化の重要性を明らかにした.また菊地はSIR理論に基づき,東京都の日毎陽性者とその累計から感染拡大期における感染率と検査・隔離率を推定し,自粛率と検査・隔離率との関係が縮小速度に及ぼす影響を解析した.その後SIQRモデルに基づく小田垣の論文(2)により,検査・隔離率の増加が重要であるという筆者等の主張と同じであることを知った.そこでこれらの内容を第1報論文「新型コロナウイルス流行に関する数理モデルとその抑圧対策について」(3)として公表した.またその後,東京都における3月から5月半ばにかけての新型コロナウイルス流行拡大・縮小期全体の解析を行うとともに,その後の再燃傾向に対する対策について考察し,その結果を第2報論文「東京都の新型コロナウイルス流行に関する解析と今後の抑圧対策について」(4)にまとめた.
6月以降,長期自粛による社会・経済活動の疲弊と破綻を止めるために,再燃を防ぎつつ社会・経済活動の段階的復帰が探索されている.日毎の新規陽性者を東京都の自粛解除条件以下に抑え再燃を防ぐことができるか,さらに完全にコロナ感染者を隔離し,正常な社会・経済活動を取り戻すことができるか否かが最大の関心事になっている.そこで本報告では,第2報の内容を紹介するとともに,7月下旬現在における急速な感染拡大状況に対して,第2報より深化した理論的立場からその抑圧対策を提案する.まず2章では,感染症流行の基礎数理モデルを示し,これから帰結される市中感染者,日毎陽性者などと感染率と検査・隔離率の基本的な関係について論述する.次に3章では,SIR理論に基づき,東京都の新型コロナ流行の拡大期から縮小期にわたるシミュレーションにより感染率,検査・隔離率,日毎の市中感染者とその累積の推移を定量的に明らかにする.4章では,東京都のコロナ再燃を防ぎつつ社会・経済活動を回復するための検査・隔離体制の在り方について考察し,限られた検査・隔離率の枠内で自粛率を変化させ再燃を抑圧する具体的な方法を示す.また検査体制を大幅に拡大し,経路不明な陽性者を含む十分大きな組織ないし地域集団の全員を検査することがコロナ感染症を抑圧し本来の社会・経済活動を取り戻す方法であることを示す.
2.新型コロナ感染流行の数理モデルとそれに基づく感染症抑圧対策の在り方
まず3,4章で述べる新型コロナ流行における感染者数の増減を支配する感染率と検査・隔離率の効果を理解するための基礎理論を述べる.本理論モデルは,感染病流行に関して,1927年にW.O. KermackとA.G. McKendrick(5)によって発表されたSIR理論モデル(S : Susceptible,感受性保持者,I :Infected, 感染者, R : Recovered 免疫保持者または Removed 隔離者)において,S を一定とみなしたときのIR理論に相当する.
2.1 数理モデル
近似的に一定の人口をもつ都市の市中に潜在している感染者(以後市中感染者という)の数を I(d) とする.ここで d は日付を意味する.市中感染者 I(d) の中の一人から,一日に他人に感染させる人の割合を感染率 b と定義する.感染者の中には他人に感染させない人および自然治癒する人もいるが,これらの効果をも含んだ平均的な感染率である.PCR検査等によって陽性者として検出され隔離される日毎の人数の,I(d) に対する割合を検査・隔離率 g と定義する.感染者は発症の数日前から発症後1週間程度の間に他人に感染させるといわれており,検査・隔離は発症してから数日後に行われるので時間的に遅れがあり,それが感染率を高め又は検査・隔離率を下げている.ここではこれらの効果をも含んだ意味での検査・隔離時における感染率とみなす.そうすると,一日当たりに市中に増加する感染者数の割合は (b−g ) なので,一日当たりに増加する感染者数 DI(d)/Dd は (b−g )I(d) で表わされる.ここで Dd は1日を表わす.これを解くと,I(d) は次式で与えられる.
I(d) = I0 e(b − g )d —- (1)
ここで e は自然対数の底であり,また I0 は d = 0とした基準日の市中感染者数である.次に,市中感染者数 I(d) の中からPCR検査等により陽性と判定されて隔離される日毎陽性者数を DR/Dd で表わすと,次式で与えられる.
DR(d)/Dd = g I(d) = g I0 e(b − g )d ——- (2)
ここで R(d) は検査・隔離された日毎陽性者の累計数で,式(2)を積分して初期値をR0 とすると次式で与えられる.
R(d) = I0g {e(b − g )d − 1}/(b – g )+ R0 —– (3)
式(1), (2)は基準日から d 日まで感染率と検査・隔離率が一定と仮定した場合の積分解であるが,b ,g がある期間ごとに変化する場合には,それぞれの期間における解を逐次乗算していけば全期間における市中感染者数,日毎陽性者数とその累計数を計算できる.
2.2 基礎式から理解できる市中感染者数増加のメカニズムと感染者抑圧対策の在り方
以下に,上記基礎式から導かれる市中感染者増加の基本メカニズムと日本および東京都のコロナ拡大・縮小過程でとられた感染拡大抑圧対策の意味を考察する.
(1) 式(1)から,市中の感染者数 I(d) はb −g > 0 ならば日数dに関して指数関数的に増加し,検査・隔離率 g を感染率 β より大きくしなければ感染者数は常に増加する.ここでは即時的な感染者増減傾向を示す実効再生産数としてRt = b / g を用いる(6).上記の DI(d)/Dd = (b / g − 1) g I(d) より,この実効再生産数 Rt は,新たに隔離される人数に対する感染する人数の比を意味し,Rt < 1とならなければ市中感染者数は増加することになる.ここで,感染率b の概算値ついて考察する.対策専門家会議のデータ分析によれば,感染者の80%は他人に感染させていないとのことなので,b = 0.2 とすると,g = 0 の場合には,d = 4 なら,e0.2×4= 2.2 となり3日以内に隔離されないと一人以上の人に感染させることになる.これから検査・隔離率を大きくすることが感染率を下げることと同程度に重要であることが分かる.
(2) 緊急事態宣言直前においては,図1に示すように,東京都の日毎陽性者のうち感染経路の不明な人の割合が75%程度に増加していた.そこで b と g の関係を推定すると,g は感染者の中で感染経路の明確な人の割合であると考えることができ,「g / b = 感染経路の明確な人数/日毎陽性者数」が概ね成立すると推察される.これから g = (1−0.75) b = 0.25b とすると,Rt = b / g =4 となる.また DI(d)/Dd = (b − g ) I(d) は,新たな市中感染者は感染経路が不明な人および見逃された濃厚接触感染者によって生じていることを意味する.一方,感染経路がすべて分かり感染者が全て隔離される場合には,b − g = 0 すなわち Rt = b / g = 1 となる.これは,多数の新規感染者が生じてもそのすべてが検査・隔離されれば,感染と隔離の間に数日の遅れがあるものの,平均的には市中感染者は増加しないことを意味する.日本の感染者探索方式,即ち新規陽性者の濃厚接触者を未来とともに過去に遡って追跡・検査し,関係する感染者全員を隔離することができた場合にはこの条件が成立していたと考えられる.
(3) ここで重視すべきことは,日本全体の社会・経済活動を縮小し b を下げるための経済的損失と g を同じ量だけ上げる医療体制強化のための経済的負荷とを比較すれば,g を上げるための経済的負荷の方が圧倒的に小さいことである.よってコロナ感染対策として当初から検査・隔離の経済的重要性を自覚し,g を高めるための体制準備が政策として重視されていれば,社会・経済活動の縮小期間をもっと短くでき,経済的打撃を低減できた可能性があったといえる.
(4) 自粛により感染率 b を g より十分小さくし,Rt = b / g < 1を長く維持すれば,増加した市中感染者をゼロ近くまで低減できる.しかし日毎陽性者数をゼロにすることができても検査・隔離されるまでの間に感染させてしまった市中感染者が存在する.また経路不明な感染者がいれば b > g の状態が続いており,やがて日毎陽性者が急増し再燃することになる.5月末の感染症流行収束期以降におけるこの問題に対する具体的な対策法については,4章で考察する.
3. SIR理論による東京都における感染率βと隔離率γの同定と市中感染者等の推定
SIR理論では,S, I, R の3変数の変化を以下の連立微分方程式で表わす(1).
dS/dt = −b SI ——–(4),
dI/dt = b SI− g I ——(5),
dR/dt= g I ———-(6)
SIRモデルでは感染による感受性保持者S の減少を考慮し,S の一人当たりの感染率を b とし,市中感染者 I が生じる感染率が b S に比例すると考える.以下に示す計算結果は,感染率 b と隔離率 g を時間的に変化させ式(4)~(6)の3連立微分方程式を時刻歴積分している.しかし東京都の新型コロナ流行の全区間におけるSの変化は,後の計算結果では初期人口の1/100の以下であり,S は全人口にほとんど等しく一定と見なしてよい.よってSIRモデルによる計算結果は2章で述べたIRモデルで評価することができる.そこでSIRモデルにおける計算結果のb Sを単にb と表記する.式(4)~(5)は,一日 D d の1/10を離散時間 Dt としてルンゲ・クッタ・ギル法で数値積分した.また計算された日毎陽性者数 DR/Dd を簡単に Rd と表記する.
3.1 東京都の感染者発生状況と東京都および政府の施策
図1は東京都のホームページに公表されている,PCR検査により陽性であることを医師が確認した日別に整理した感染者発生状況である(7).図1には,東京都および政府が発令した要請や宣言の期日も併記した.これらの要請や宣言は日毎陽性者数の変化の節目に影響を与えている.
3.2 拡大・縮小期の曲線適合による b とg の同定
第一の課題は,図1の日毎陽性者とその累積の実際値から,未知のパラメータである感染率 b と検査・隔離率 g を同定し,市中感染者 I 等を算出することである.日毎陽性者数は,指数関数的に増加するので,片対数グラフ上で解析する.パラメータの同定は以下のように行った.(1)日毎陽性者数の実際値 Rd に対して,片対数グラフ上で最小二乗法によって導出した直線的に変化する領域の勾配から,(b – g )の値を求める.(2)導出された(b – g )の直線に滑らかに接続するようにb ,g を変化させて,数値積分を行い,日毎陽性者 Rd と累計陽性者数R の計算値がそれぞれの実際値に適合する曲線を求め,そのときのb ,g を最適同定値とする.

図1 東京都の感染者発生状況(7)と東京都および政府の施策
図2に示す曲線は,日毎陽性者数の拡大・縮小期に対して上記(1), (2) の手順を基に,多くの試行計算の後に最終的に得られた最適曲線である.この結論に至った試行過程の詳細は論文(4)を参照されたい.まず拡大期については,Rd が10人以上となる3/24以降から4/1頃までの平均増加特性は直線 b – g = 0.11 (図2中の黒破線 a)で表わされる.Rd は週当たり2.1倍で増加している.3/24以前も含めた曲線適合計算から,拡大最後期の感染率 b と検査・隔離率 g をそれぞれ b0, g 0と表わすと,最適同定値は b0 = 0.14, g0 = 0.03となる.式(2)ないし(6)から,図2で赤線の市中感染者 I は Rd / g で与えられ,この拡大最後期には Rd の33.3倍で増加した.

図2 感染拡大・縮小期における日毎陽性者数 Rd,累計数 R の実際値とその適合曲線,市中感染者数 I の計算値,感染率 b と検査・隔離率 g の同定値,および収束期以降における I と Rd の予測特性
感染爆発を防ぐために3/25に発せられた都の外出自粛要請を契機に増加速度が低下し,やがて縮小期に移行した.縮小期の Rd の平均減少特性は途中で変化する.そのため前半の4/14~4/20の 間のRd の平均減少傾向を b – g = – 0.083(茶破線 b)と同定し,この値がこの期間継続するとみなした.一方,後半の5/4以降の平均減少傾向は b – g = – 0.13と同定した.
Rd の拡大期から極大を経て縮小前期まで,および縮小前期から後期に Rd と R の実際値に曲線適合する b と g の変化は,図2の下部に示した.まず感染率 b は,都の外出自粛要請により3/26から4/14にかけて b0 から 0.05b0 (b = 0.007) に線形的に減少し,その後一定に維持される.
ここで自粛率を自粛要請以前の感染率 b0 からの感染率の低下率と定義すると,1−0.05 = 0.95となるので,自粛率95%になる.一方検査・隔離率 g は,4/1から4/14にかけて g 0 から 3g 0(g = 0.09)まで線形的に増加し,その後4/20まで 3g0 に維持されるが,4/20から5/4にかけてさらに 4.57g 0(g = 0.137)まで線形的に増加し,5/4以降は 4.57g 0 が維持される.この条件におけるRの計算値は実際値とよく一致(4/1~5/17の期間における誤差比の標準偏差は3.5%と僅少)しており,同定された b と g の変化は信頼できると考えられる.95%の自粛による感染率 0.05 b0 = 0.007 の妥当性については,既報(4)において推定された自然治癒率 d = 0.02 を考慮すると,自然治癒率を除いた感染率は b0 + d = 0.16 から0.027まで低下したことになり,実効的な自粛率は83%であったと推察される.一方検査・隔離率 g の変化の妥当性については,厚生労働省のホームページの資料(8)によれば,4月初めから地方衛生研究所・保健所および国立衛生研究所のPCR検査数が大幅に増加すると共に,民間検査会社の検査数も急増しており,このことが検査・隔離率 g = 3g 0 への増加をもたらしたと考えられる.更に4月下旬には検体検査が歯科医師にも認められ,大学および医療機関によるPCR検査も加わったことが連休後半にかけて g = 4.57g 0 まで増加した要因と推察される.また5月初旬頃からは発症から検査に至る期間が短縮されたことも検査・隔離率の向上に寄与していると考えられる.
なお,図2からも理解されるように,日毎陽性者Rdが10人程度以下になると,統計的な平均値を対象とするSIR理論は適用できない.この領域では局所的な集団感染,3密に近い経済活動,散発的な経路不明な感染者の発症が日毎陽性者数を支配するからである.しかし5/20頃から6月下旬にかけて,紫線で示すように,一定の増加率でRdが増大している.この増加指数は b −g = 0.049で,週当たりの増加率は約1.4倍/週となる.ここで g は 4.57g0 に維持されているとすると b = 1.33b0,Rt = 1.36となり,SIR理論から,100人を超える市中感染者 I が1.4倍/週の増加速度で生み出されていることになる.
一方, g = 4.57g0 を維持しつつ5/8から,感染率 b が b0 および 0.8b0 に急に変化したときのRdとIの予測特性をそれぞれ緑および青の直線で示した.緑線で示す b = b0 の自粛率ゼロの場合では b0 > 4.57g0 となるので Rd,I は漸増する.しかし青線で示す b = 0.8b0 の場合は 0.8b0 < 4.57g 0 となるので Rd ,I が漸減して抑圧できる.この市中感染者が一旦収束した後の再燃現象に対する対策については4章で詳しく論じる.
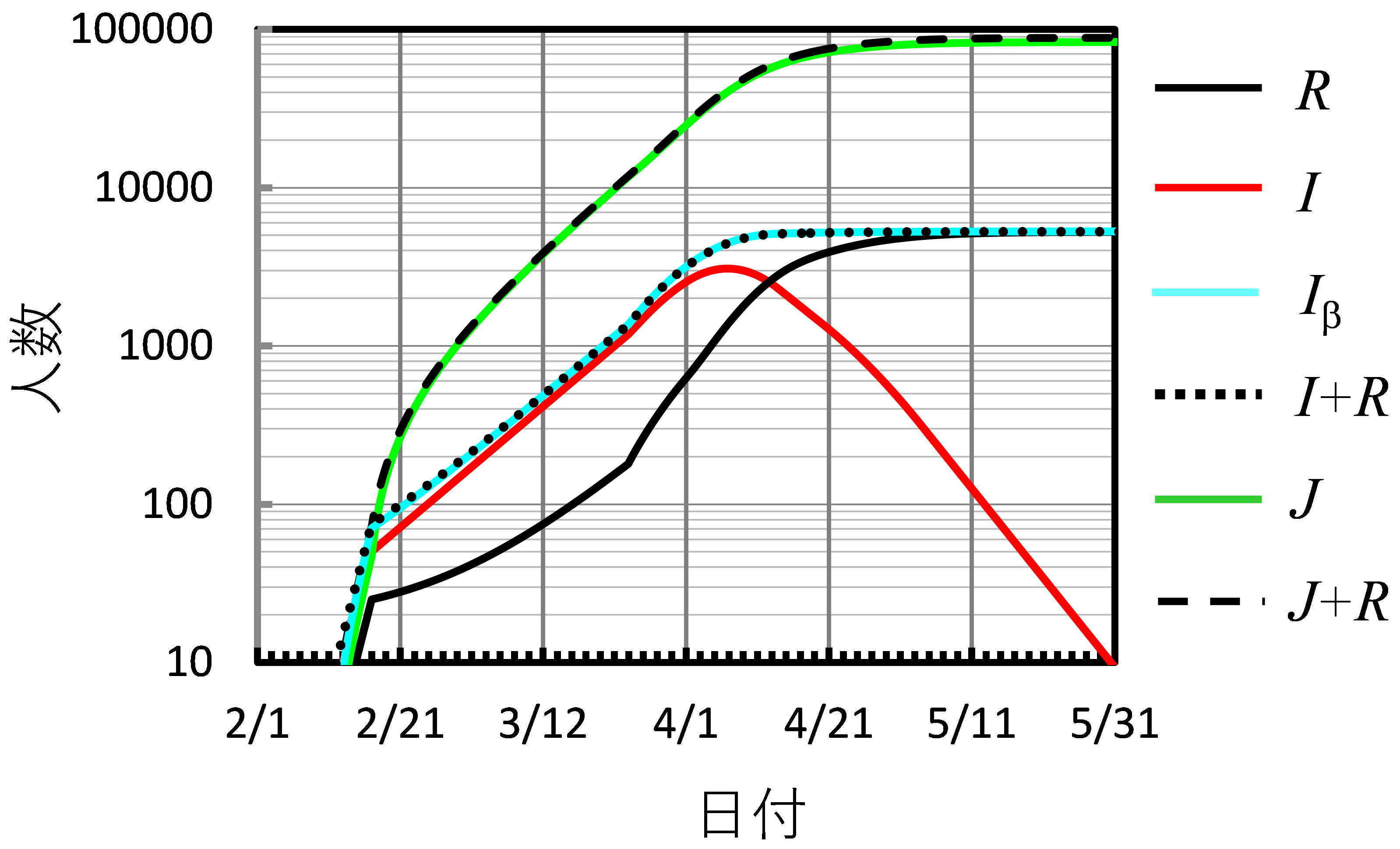
図3 感染力のある感染者数 Ib と市中感染者 I ,累積陽性者数R との関係,および感染力のない感染者累計 J と総感染者数 J + R の推移
2章で述べた基礎式から,他人に感染させる能力のある市中感染者数の累計は Ib = Σb I で与えられ,発症せず他人に感染させない市中感染者数の累計は J = Σ(1−b )I で与えられる.そこで図2に示した拡大・縮小全過程における計算値を用いて,Ib,J および I + R,J + R (=ΣI ) を計算し,I,R と共に図3に示す.図3より以下のことがいえる.① 青線と黒点線が一致していることから Ib = I + R の関係が常に成立している.即ち,市中感染者 I(赤線)は日毎陽性者累計 R (黒線)が感染力のある感染者累計 Ib(青線)に追従できない結果として増加する.市中感染者を増加させず,また早期にゼロにするには,検査・隔離能力を高めることが重要であるといえる.②黒破線で示す全感染者 J + R のほとんどは J(緑線)であり,発症し検査・隔離された陽性者累計 R は僅かである.5/25における J + R は88,440人なので,東京都総人口1,380万人(9)で除すると 0.64% で,報告されている実際値に近い値になっている.③ 収束期の5/25においては Ib = R = 5,290人で,この日の R の実際値は5,174人であり誤差 2% 程度である.これから感染能力のある陽性者 Ib = R + I は総感染者数 J + R の 6.0%に相当していることが明らかになった.
4.新型コロナ感染収束期における再発の制御・抑圧法
4.1 自粛解除レベルをあげるために必要な検査・隔離率
5月25日の緊急事態解除以降,感染防止のための新生活様式をとりながら2密,3密を避けつつ段階的な社会・経済活動の再開が行われている.しかし図1,2に示されるように,Rt = 1となる医療機関等における集団感染者は別として経路不明な新規陽性者が増加傾向にある.これは感染と検査・隔離には時間差があり,平均5~6日,長い場合は2週間の潜伏期間中に無症状のまま他人に感染させるからである.
そこで3章で同定された東京都における感染率と検査・隔離率の値を前提として,IRモデルの観点から,現在の東京都の日毎陽性者の増減状況に対して,再燃しないために必要な検査・隔離率の条件を考える.
まず式(2)の日毎陽性者数 Rd (= DR/Dd ) から,Rd の増加率および減少率は, e{(b −g )d} で決まる.そこで1週間(d = 7)当たりの Rd の増加率および減少率を考えると,e7(b–g) で与えられる.(b – g ) の値が 0.026,0.048,0.067, 0.084であるとき,e7(b–g) は,それぞれ1.2, 1.4, 1.6, 1.8倍/週で増加する(この増加率を再燃度と呼ぶ).一方,(b – g ) の値が,0, -0.026,-0.048であるとき,e7(b–g) は,それぞれ1, 1/1.2,1/1.4倍/週と減少する(この減少率を抑圧度と呼ぶ).図4は,再燃度と抑圧度における自粛率と検査・隔離率 g の関係を,横軸に自粛率,縦軸に検査・隔離率 g をとり示したものである.ここで横軸の自粛率は,自粛前の感染率 b0 = 0.14,現在の感染率を b として 1 − b/b0 で定義し,b = b0 ならば自粛率ゼロ(0%),b = 0 ならば自粛率1(100%)である.また b がb0 より大きい場合には自粛率は負となる.

図4 再燃を抑圧できる自粛率(= 1 – 感染率比 b /b0)と検査・隔離率の関係(b0 = 0.14, g0 = 0.03, g s = 4.57g0 )
図4において,抑圧度1の黒線は日毎陽性者数を一定値に抑圧できる条件を示し,感染者が増大し再燃の度合いが高いほど下方の破線にシフトする.一方,抑圧対策により抑圧効果が生じた場合,その度合いが強いほど上方にシフトする.例えば図2の紫線で示した再燃度が1.4の場合には図4の紫破線上にあり,g = g s = 4.57g 0= 0.137とすればその横線との交点から自粛率は −0.33となり,このとき感染率は b = 1.33 b0 となっている.この状態から,g を変えずに自粛率を0.2にすれば,抑圧度1の黒線の上方にある1/1.2倍/週の青線に移行し抑圧することができる(自粛率増加による抑圧).一方,自粛率は −0.33 のままで g を g = 0.212 = 1.55gs とすると,その交点である青線上に移行し,自粛率による抑圧と同じ抑圧効果が得られる.後者の場合は,自粛率が−0.33であるため自粛を要請しない社会・経済活動が可能になる.これから分かるように,図4は日毎陽性者の増加率を観測することにより,再燃させないために必要な検査・隔離率と自粛率の在り方を予測できる線図であることがわかる.
なおSIRシミュレーションにより,6月頃の感染率が b = 1.33 b0 ,自粛率 −0.33が得られたということは,社会・経済活動の自粛レベルが自粛要請直前の3月25日頃のそれに比べて低くなっていることを意味する.ただし6月中旬頃の感染率が大きくなっている要因として新型コロナウイルスが変異し感染率が高くなっている可能性もあり,今後さらに解明すべき課題である.
4.2 検査・隔離率と自粛率の変化による感染拡大の抑圧制御
東京都の日毎陽性者は,図2に示したように6月中は増加率1.4倍/週の再燃度を示したが,7月初めから下旬にかけては再燃度1.6倍/週に増加した.7月下旬現在,今後の急激な増加が危惧され,不要不急の行動自粛,事業活動の縮小が要請され始めている.今後如何にしたら社会経済活動を縮小することなく,日毎陽性者および市中感染者を抑圧制御できるかが喫緊の課題になっている.そこで図4を用いて,第1波の感染流行が収束した5/18を初期日として,それ以降11週間後の8/2までの日毎陽性者の実際の増加特性をまず模擬する.次に12週目の8月3日からの自粛率および検査・隔離率を高めることによってどのように日毎陽性者を抑圧できるかを予測する.
まず,図2に示す東京都の日毎陽性者数 Rd の平均的な変化から,5/18~5/31までの2週間の増加率は1,6/1~7/5までの3~7週間の再燃度は1.4とする.その後の Rd の実際値は図示していないが, 7/6~8/2までの8~11週間の再燃度の平均値は1.6と評価した.この1~11週間における再燃度の変化を図5の下段に赤点線で示し,それによって増加する日毎陽性者数 Rd の増加特性を上段の赤実線で示した.11週目の7/27には Rd = 352人に増加し実際に近い.
図5に示したRdの1~11週までの変化を図4で説明する.東京都の「都内の最新感染動向」(7)によると,5月下旬頃の陽性率は1%,検査人数 900人/日,6月は陽性率2%弱で検査人数 1,700人/日が維持されていた.そこでこの時期は g = gs が維持されていたと判断すると,1~2週間目までは抑圧度1の黒線と gs の黒破線の交点①近傍にある.このときの自粛率はほぼゼロで,感染率は b = b0 である.しかし3週間目(6/1~6/7)には gs と再燃度1.4の紫破線との交点③に移行し,7週間目(6/29~7/5)まではこの位置にいたことになる.この位置の自粛率は −0.33,感染率は b = 1.33b0 となる.次に8週目(7/6~7/12)から,gs と再燃度1.6の茶破線との交点④に移行し,ここで11週目(7/27~8/2)まで留まっていることになる.この位置の自粛率は −0.46で,感染率は b = 1.46b0 に増加したことになる.
次に8/3からの12週目以降の Rd の変化を模擬計算する.まず図4の再燃度1.6の茶線上の④の位置に留まるとすると,図5の赤線で示すように,Rd は1.6倍/週の再燃度で増加し,16週目の8/31~9/6には Rd = 3,696人にもなる.よって速やかに何らかの抑圧対策をとる必要がある.

図5 第2波における日毎陽性者 Rd の増加特性と抑圧法1(紫),2(青),3(黒) による抑圧特性の予測計算結果
そこで【抑圧法1】として,図5において紫点線で示すように,12週目(8/3~8/9)から1週間毎に再燃度・抑圧度を1.4→1.2 →1 →1/1.2→1/1.4と順次変化させていった場合のRdの変化を上段の紫実線で示す.この場合,13週目(8/10~8/16)の間に Rd は 約600人の極大値をとりそれ以降減少する.次に【抑圧法2】として,図5の下段に青点線で示すように,12週目(8/3~8/9)に抑圧度1に移行し,13週目(8/10~8/16) 以降は抑圧度1/1.2(図4の青線上に相当)に移行させた場合には,上段の青実線で示すように,Rdは13週目から(1/1.2)/週で低下している.さらに【抑圧法3】として,図5の下段に黒点線で示すように,12週目に抑圧度1に移行し,13週目以降は抑圧度1/1.4(図4の紫線上に相当)に移行させた場合には,図5の黒実線で示すように,Rdは13週目から(1/1.4)/週で低下し,8月末には100人以下になる.
市中感染者Iと日毎陽性者Rdの抑圧法として3つの代表例を示したが,図4を用いると,それぞれの抑圧法において,検査・隔離率と自粛率(感染率)の制限条件を考慮しつつ効果的な経路を考えることができる.まず【抑圧法1】を実現するために,再燃度 1.6(b = 1.46b0)で g = gs の④の位置から順次再燃度を下げていく経路を考える.社会・経済活動を維持したままでこの抑圧法1を実現できる最も望ましい施策は,自粛率 −0.46の縦直線と再燃度(1.4,1.2)・抑圧度(1,1/1.2,1/1.4)の各斜め線との交点に沿って g を逐次 0.156(1.14gs)→0.178 (1.30gs ) →0.204 (1.49 gs)→ 0.230 (1.68gs )→0.252 (1.84gs )と高めていく経路である.これに対して,g = gsのままで g を上げる対策をとれない場合には,g = gs の横線と各再燃・抑圧度の斜め線との交点に沿って,自粛率を逐次 −0.322 → −0.164 →0.021 →0.207→0.365(感染率 b はそれぞれ,0.185,0.163, 0.137, 0.111, 0.089に対応する)に高めていく経路となる.この2つの経路以外に多数の選択肢がある.例えば最初はg = gs の線に沿って再燃度 1.2 の交点まで移行して自粛率を −0.164 まで高め,その間に検査・隔離体制を整備して,自粛率 −0.164 の縦線と各抑圧線との交点にそって検査・隔離率 g を増加していくことができる.
次に【抑圧法2】を実現するためには,まず g = gs に沿って抑圧度1の黒線との交点に移行し,次に抑圧度 1/1.2 の青線との交点に移行する経路が考えられる.しかしこの間に検査・隔離率を高める体制を整え,g の値を高めることができれば,g の横線と抑圧度 1/1.2 の青線との交点上で自粛率を低下させ,g の増加と共に社会・経済活動を緩和することができる.最後の【抑圧法3】を実現するためには,まず g = gs に沿って自粛率を高め,抑圧度1に移行し,1週間後に抑圧度 1/1.4 の状態に維持する方法がある.しかし検査・隔離体制を強化し検査数を逐次増加することができれば,紫実線に示す抑圧度 1/1.4 の線に沿って自粛率を再び低下させることができる.
以上の考察から,社会・経済活動と感染抑圧活動を両立させるためには,検査・隔離率を増加することが必須であることが明白である.検査・隔離率を現状の2倍に高めることができれば,現状の自粛率においても感染拡大を抑圧できると予想される.検査数の増加,接触検知アプリの導入等により検査・隔離率を更に高めることによって社会・経済活動の自粛度を更に緩和することができると推察される.
4.3 感染後に検査する因果律を克服し,g ≧ b を実現する検査・隔離方法
すでに4.2節で述べたように,予想される感染率 b に対して日毎陽性者の増加率を抑圧するに十分な検査・隔離率 g を実現できれば再燃の抑圧が可能と考えられる.もしクラスターが発生しても感染者と濃厚接触者の追跡が可能な場合には感染を抑圧できる.しかし感染経路が不明な感染者が多くなれば,経路不明な感染者に対する別の抑圧対策しなければならない.この経路不明な感染者の存在によるウィズ コロナの生活をから解放されるためには,常に g ≧ b が成り立つ方法を探索することである.それを実現するためには,経路不明な陽性者が現れたとき,その陽性者を含む組織,即ち医療機関,福祉施設,学校,企業,家族が属する特定の地域住民などを対象に一斉にPCR,抗原検査等をして,経路不明の人より多い無症状の潜在的感染者をも見出して積極的に g ≧ b とすることである.医療機関や福祉施設で陽性者が発見されたときには,病院,施設のすべての従事者と陽性者の家族を含めた全員の検査がなされてきた.しかしここで提案するのは,学校,企業,繁華街等で新規陽性者が見出されたときには,それらの組織や地域に属する人をその家族をも含めてPCR等の検査をすることである.そして無症状の感染者をその集団から検査・隔離できれば,教育,各種企業・業者,地域産業の活動を止める必要がなくなる.特にコロナ感染者の治療に全力を尽くしていただいている指定医療機関の従事者に対しては,前述の潜伏期間における無症状者による感染のリスクをなくすためには3日に一度の定期PCR等の検査が必要であろう.また小・中学校,高等学校において,陽性者が発生した場合でも,これ以上の教育の遅れを生じさせないことが重要である.付属病院をもつような大きな企業では,すでに独自でPCR検査や抗体検査を行い,正常な企業活動を実現する努力が行われている.発症者に対する検査のみでは,必ず感染経路不明者が現れ b > g となるので,経路不明な陽性者を含む組織,自治体等に属する集団を検査することにより,g ≧b が満たされるまで潜在的な感染者を探索することが重要である.
中国の武漢では,5月14日から19日間にわたり市民約990万人にPCR検査を実施し,300人の無症状陽性者を見出した.残存陽性者が他人に感染させない感染者のみであったとすれば,発症者の経路追跡探索は勿論のこと,ここで述べたような一人の経路不明者でもそれを含む大きな集団のPCR検査をしていたためであろうと思われる.
厚生労働省は5月29日に,新規感染者の濃厚接触者は症状の有無にかかわらず全員PCR検査を実施すると発表した.また基本的対処方針等諮問委員会では第2波に備えて,一日に10~20万件の検査医療体制を秋までに整備すべきと提言している. 6月2日には唾液検査方式も認可され,今後自動PCR検査機も導入される計画である.また下水をPCR検査することにより,特定の組織および地域集団の陽性者を発症の1週間前に検出できることも明らかにされた.これは g ≧ b を目指した組織集団や地域住民全員のPCR検査のための有力な手段になる.新生活様式による自粛率ゼロを維持しつつ g ≧ b を実現するには,東京都だけでも当面10万件/日,全国で50万件/日のPCR検査体制の構築を目標とし,直ちに開発に着手すべきである.これにより経路不明な発症者及び無症状の感染者を含む大きな集団にPCR検査を実施するとともに,医療機関,福祉施設,行政機関,教育機関,企業体等が正常な活動を取り戻すに必要なPCR検査を随時実施できるようになれば,東京都も安全な都市になると思われる.
今年の秋・冬には新型コロナの第2波が来ると恐れられている.しかしすでに7月末現在,東京都および主要都市圏において,日毎陽性者が急増し第2波が到来しているといえる状態である.これを抑圧するためには適度の自粛を実施しつつ検査・隔離体制と医療体制を強化することが急務であると思われる.
5. あとがき
本論文では感染症流行に関する最も簡単な数理モデルに基づき感染症流行のメカニズムを解説し,それから帰結される検査・隔離率の重要性を論じた.また東京都の感染者拡大・縮小過程をシミュレーションし,感染率,検査・隔離率,市中感染者とその累積の推移を定量的に明らかにした.次に同定された感染流行収束期の感染率と検査・隔離率を基準として,感染再拡大による再燃度とそれを抑圧するための抑圧度を社会・経済活動の自粛度と検査・隔離率との関係として定量的に示した.また7月下旬の感染流行拡大状況に対して,社会・経済活動の適正規模の自粛とともに,検査数を極力多くし検査・隔離率高めることにより再発の山を縮小させる抑圧法を示した.さらに組織および地域に属する経路不明な無症状感染者を含むすべての人を検査・隔離することにより,正常な社会・経済活動が実現できる可能性を示した.
本論文の詳細は論文(4)で述べているが,論文(4)の4.1, 4.2節の説明と図11は誤りであることが分かり,本論文ではこれを修正するとともに,6月中旬と異なる7月下旬現在の感染症流行状況に対する抑圧対策法を論じた.なお機械学会誌に寄稿した本論文の紹介文も論文(4)の誤った説明を用いている.ここにお詫びして訂正させていただく.
本稿が,新型コロナ流行現象の科学的理解を深め,その合理的、具体的な抑圧対策の指針となれば幸いである.
謝辞
本研究を進めるに際し,活発な相互討論と情報交換や校閲に協力いただいた佐藤勇武氏(元NTT/TDK/(医)徳枝会)に感謝します.
続報
本稿の続報を下記に公開する
東京都のCovid-19第5波 感染拡大・縮小過程のSIR理論解析(2021年12月2日)
東京都における新型コロナウイルス第5波の感染拡大・縮小の主要因の分析とウイズコロナ社会実現への期待(2021年10月12日)
新型コロナ感染症の第5波の感染拡大の主原因は何か? 第2部:IR理論による詳しい分析結果(2021年8月25日)
新型コロナ感染症の第5波の感染拡大の主原因は何か? 第1部:7月末の感染拡大の解析(2021年8月2日)
東京都における新型コロナウイルス感染症第3波流行の分析と対策について(2021年1月29日)
東京都における新型コロナ感染症流行の12月24の状況分析と対策について(2020年12月27日)
新型コロナ第3波の状況分析と対策は?(2020年12月4日)
執筆者プロフィール
<名誉員>
小野 京右 東京工業大学 名誉教授
◎専門:機械力学,トライボロジー
<名誉員>
菊地 勝昭
◎専門:機械力学
参考文献
(1) 西浦博・稲葉寿, 感染症流行の予測:感染症数理モデルにおける定量的課題, 統計数理, Vol. 54,No. 2 (2006), pp. 461−480
(2) 小田垣孝,新型コロナウイルスの蔓延に関する一考察,物性研究・電子版,Vol.8, No.2 (2020), http://mercury.yukawa.kyoto-u.ac.jp/~bussei.kenkyu/
(3) 小野京右・菊地勝昭,新型コロナウイルス流行に関する数理モデルとその抑圧対策について, 2020年5月21日,https://blog.hatena.ne.jp/KyONO
(4) 小野京右・菊地勝昭,東京都の新型コロナウイルス流行に関する解析と今後の抑圧対策について, 2020年6月15日,https://blog.hatena.ne.jp/KyONO
(5) W. O. Kermack and A. G. McKendrick, A Contribution to the Mathematical Theory of Epidemics, Proc. Roy. Soc. of London. Series A 115 (772) (1927), pp. 700−721
(6) 稲葉寿,感染症の数理,「医療とアクチュアリー」講演 (2009/3/18)
(7) 都内の最新感染動向,東京都の新型コロナウイルス感染症対策サイト, https://stopcovid19.metro.tokyo.lg.jp
(8) 厚生労働省ホームページ,国内における新型コロナウイルスに係るPCR検査の実施状況(6月11日時点), https://www.mhlw.go.jp/content/10906000/000639750.pdf
(9) 総務省統計局ホームページ,人口推計 平成30年10月1日現在, https://www.e-stat.go.jp/dbview?sid=0003312321
