密閉円筒容器内に流体を満たし、下面を一様に加熱し上面を冷却する。熱は上下間の温度差が小さい場合には熱伝導によって伝わり、温度差が大きくなると流動が生じて熱の移動がおこなわれる。この現象を支配する無次元数は上下面の温度差に基づくレイリー数であること、流動パターンはレイリー・ベナール対流であることは周知のことであろう。また、単純化された系としてのローレンツモデルがその非線形項のために、カオスを生み出すことも広く知られている。

数が大きくなると（）、規則的なロールパターンは崩壊し、やがて不規則な流動状態が出現する。この状態を熱乱流と呼ぶこととする。熱乱流状態を特徴づけるパラメータとしては、ヌッセルト数と数の関係があり、両者はとなることが古くから提案されていた。しかし９０年代になると、より高い数（）では、ベキ指数がからわずかに小さくなることが実験的に報告されるようになった。その原因として、熱乱流状態はまったく無秩序な運動をしているのではなく、その中には自発的に形成される秩序的な流動が存在することが考えられている。この運動は容器全体にわたる流動を引き起こすため、巨視的流動と呼ばれる。巨視的流動がどのような原因から形成されるのかは、興味深い課題ではある。 しかし、本稿ではいったん形成された流動に焦点をあて、本特集のテーマである「非線形」と関連させながら、著者らの実験で得られた知見を紹介したい[1][2]。

古典的な課題である対流がふたたび注目されることとなった要因として、高い数での実験がヘリウムを用いて可能になったことがある[3]。数多くの研究から、において発達した乱流状態が出現することが見出された。それは、従来の熱乱流が持つ性質と統計的に異なっていたため、新たに「ハード乱流」と名付けられた。一方、において観察される乱流状態は、「ソフト乱流」と呼ばれる。前者は容器中心部における温度変動の確率密度関数が、すそ野が広がる指数型になる。これは、非常に高温（低温）の流動が、確率は低いが間欠的に中心部の温度変動に寄与していることをあらわしている。後者では確率密度関数型はガウス型になる。

カダノフは、ハード乱流を理解するための流動を提案しているので、それを紹介しておこう[4]。図１は、容器の中心部をとおる断面内を模式化したものである。上下面ではキノコ雲状のプリュームが生成され、それらは一部が中心部へ放出されるとともに一方の壁に移動して、側壁にそった強い上昇（下降）流を形成する。つまり、この一連の過程：プリュームの発生 -> 移動・合体 -> 側壁への衝突 -> 上昇（下降）流の形成、が容器中心部の乱流をより発達させることとなる。また、流動の影響は容器全体に及ぶことは明らかで、この流れが本稿で対象とする巨視的流動である。

巨視的流動の存在は、熱の輸送にも少なからず影響を与えることが予想される。上下面近くには速度（及び温度）境界層が形成される。乱流の支配方程式を考えると、境界層では粘性項が支配的になるが、中心の発達乱流場では慣性力が中心的役割を担う。従来は中心領域と境界層という二層のモデル化がなされてきたが、Castaingらは両者をつなぐ領域に混合層の存在を仮定した[5]。混合層では粘性項と浮力項が釣り合い、中心領域では慣性項が浮力項と釣り合うオーダー評価から、ヌッセルト数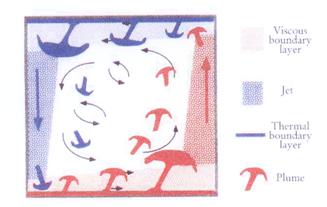と数の関係はと見積もられている。また、容器中心部における温度（）と速度の変動強度（）に関しても、次のようなスケーリング則が提案されている ：, 。

図 1　Kadanoffらの流動モデル[4].円筒容器垂直断面内の模式図．

図２に実験装置の概要を示した。作動流体は、水と水銀である。装置寸法および作動流体として水銀を用いる場合の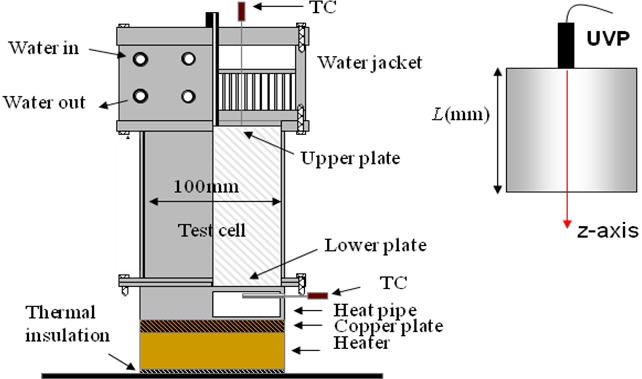数を表１にまとめてある。達成される最大数は、である。試験部はステンレス製で、下面をヒートパイプによって一様加熱し、上面は循環水により除熱する。速度計測には、粒子画像計測（ＰＩＶ）法、超音波流速計測（ＵＶＰ）法を用いた。上部に設置したＵＶＰセンサにより、中心軸上の128点の変動速度を同時計測する。ただし、変動はセンサに向かう方向（マイナス）と遠ざかる方向（プラス）の一次元成分しか計測できない。円筒中心に小型サーミスタ（直径0.25mm）を設置して、速度と温度の同時計測をおこなった。作動流体として水を用いる場合にはアクリル製の試験部として、ＰＩＶにより垂直断面および水平断面における二成分速度の計測をおこなった。巨視的流動が通過する面を便宜上、循環面と定義する。ＰＩＶ計測を効率よく行うためには、循環面の方向を事前に知る必要がある。 そのため、円筒容器は微小角度だけ傾きをもたせてある。この方向をx軸と定義し、残りの垂直軸をy軸とする。

図 2 実験装置概略．PIV計測をおこなう際には、アクリル製容器を用いる．


表１　装置寸法と数．

3. 巨視的流動（ ）

密閉容器内に巨視的な流動が存在することは、自ら実験データをとるまでは半信半疑であった。それは、発達乱流中に存在する組織構造（秩序構造）に関して学んだ経験があれば、組織構造を客観的に見出すことがいかに困難であるかを知っているからである。私が大学院の時代には乱流中の組織構造の議論が活発に行われていたが、結局のところ、どのような手法を用いて構造を抽出するのかが問題で、組織構図の全体像を満足に捉えることはできなかった。その後、流体の計測方法は格段に進歩した。本稿では、ＰＩＶ法、ＵＶＰ法を用いたアスペクト比１の結果を紹介する。

巨視的流動は、図１に示すような反時計回りの流れが定常的に存在するわけではない。ある時間帯で上昇流がおこり、しばらくして下降流が形成される。中心部の流れは、側壁の上昇流と下降流に互いに加速されるように乱流が発達する。この状況はしばしば、はずみ車が加速される状況にたとえられる。図３には、円筒の中心軸をとおる垂直断面内の流動をＰＩＶ計測したもので、上昇流が優勢な時間帯と下降流が優勢な時間帯の一例を示した。このような画像は、巨視的流動の循環面を見いだせれば容易に撮影できそうであるが、次項で述べる理由から、それほど容易ではなかった。右図は長時間平均した場合のベクトル図であり、この画像を見ると容器を循環する大きな平均流れとして巨視的流動を特徴づけることもできる。

図 3　巨視的流動の上昇流および下降流の優勢な場合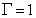（）．右図はその長時間平均のベクトル図．

図４は容器内の壁付近で計測された速度変動の周波数スペクトルである（作動流体は水）。上面、下面、側壁いずれの位置においても明確なスペクトルピークが存在することから、上昇（下降）流は周期的な変動をすることがわかる。そのピーク周波数をとする。は数に対してベキ乗で変化する（）ことが知られており、その指数はである。さて、容器中心部において同様の周波数スペクトルを計算してみたところ、y軸方向にもっとも顕著なピークがあらわれ、x軸方向にもわずかなピークが認められた。しかし、z方向速度の変動には周波数ピークを認めることができなかった。 つまり、側壁付近では上下方向（z方向）の速度変動が存在するが、その影響は中心部ではy軸方向とx軸方向に限られることとなる（ただし、水銀を用いた場合には、傾向は異なる）。この結果は、巨視的流動のパターンを考える上で重要なポイントであったが、当初は予想外の結果であった。巨視的流動は二次元面内の運動をするのではなく、三次元的な流動をすることが想定される。そこで、次に述べる水平面内の解析を行ってみた。

図５は上部プレートから5mmの位置における水平断面内の流動のＰＩＶ計測画像である。ベクトルは流動の方向をあらわし、色はその大きさを示す（暖色が大きい値に対応する）。側壁付近で上昇流が湧き上がり、上面を流れる様子がよくわかる。さて、円筒中心部（破線の正方形）を切り出して、その領域内でのベクトルの平均を計算してみる。この平均ベクトル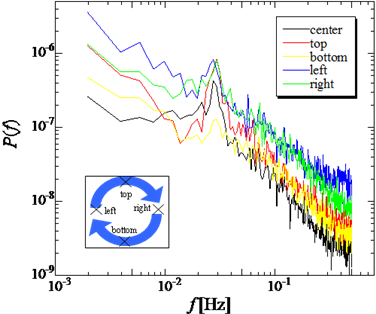が座標系の基準軸となす角度をと定義する。巨視的流動が、いつも同一の循環面内を流動していれば、である。しかし、実測されたは、図６に示したように時間的に変動する。その変動の揺らぎは大きいが、周期的（）であることがわかる。つまり、巨視的流動は二次元的な運動しているのではなく、循環面は周期的に振動していることが推測される。この振動が、円筒中心におけるy軸方向の顕著なスペクトルピークをもたらしたことと理解できる。循環面の振動は、巨視的流動の１つの安定な状態と考えられる。 しかし、の変動は大きく何らかの原因で突発的に流動の循環方向が反転する現象が確認される。例えば、模式的には図６に示したように安定な状態が別の安定な状態に遷移するわけである。 反転がおこる時間スケールは、きわめて長く振動周期の数百倍にも及ぶ。近年、反転現象を説明する非線形なモデルが考案されつつあるが、物理的原因はまだよくわかっていない。

図 4　容器内の各位置で観測される周波数スペクトル（,）．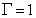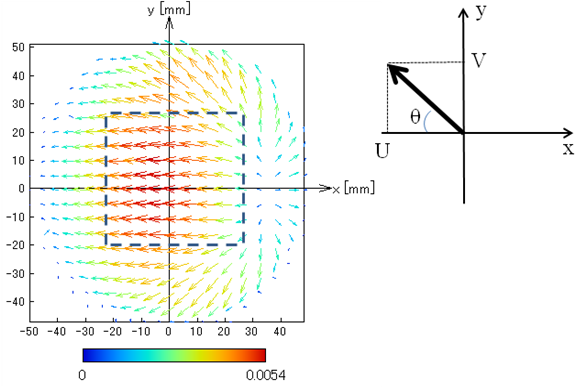


図 5　容器情面から5mmの水平断面における流速ベクトル．


図 6　水平断面内における巨視的流動方向の時間的変化（,）．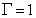

4. 巨視的流動（,）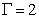

これまでは、アスペクト比１の円筒容器における巨視的流動を紹介してきたが、アスペクト比を変化させた場合にも、巨視的流動の存在は確認されている。しかし、流動パターンはより複雑化を呈する。図７にはＵＶＰにより計測された中心軸上の変動速度を計測時間に対してプロットしたものである。縦軸はセル高さで無次元化してある。等値面の暖色は下降流、寒色は上昇流を表す。右側のグラフは平均速度分布であり、自由落下速度（ 、は熱膨張係数）で無次元化してある。では、上昇流と下降流が周期的に繰り返しその影響は容器全域に及んでいる。一方、では、下面へは下降流、上面へは上昇流が形成される結果となった。これはとは逆の傾向であり、我々の常識に反する結果である（興味があれは、流動パターンを想像してみてください）。詳細は文献[1,2]を参照していただき、注目すべきは、上面付近の流れが下面に影響を及ぼすことはないことである。 では、上昇流と下降流は密接に関連しており、つまり上面と下面における現象は相互に関連をもっており、その情報伝達によって図６に示した循環面の振動が起こると予想される。 もちろんそれは非線形な相互作用が働いていることは明らかで、この点に注目したモデル化も進められている。では下面の情報は直接に上面（もしくはその逆）に伝わることが予想され、では上下面間の情報が交換される可能性は極めて少ない。

巨視的流動は、アスペクト比によって大きく異なることが予想されるため、その流動パターンを体系的に理解するには、まだ時間がかかるであろう。巨視的流動を記述する共通の性質は何なのか？普遍性はあるのだろうか？それが今後の研究課題なのかも知れない。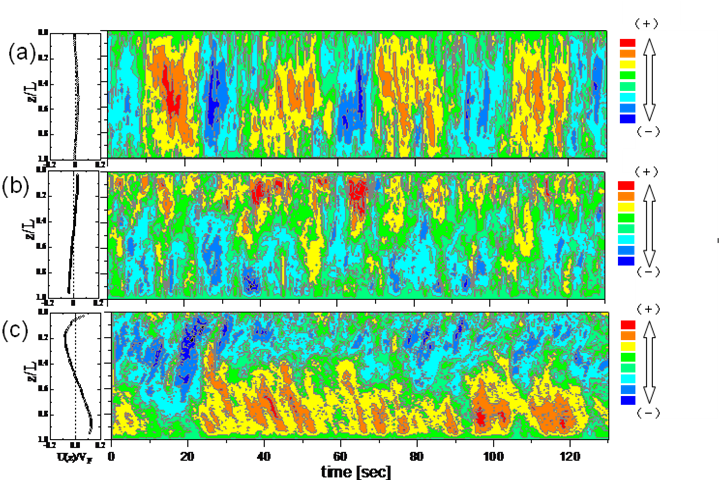

図 7　ＵＶＰにより計測された円筒中心軸上の速度変動の時間的変化.マイナス符号が上昇流、プラスが下降流をあらわす.(a)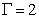,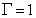(b) ,(c) .

密閉容器内に形成される巨視的流動パターンに焦点を当て、その簡単な紹介をした。本稿では触れなかったが、熱乱流に関しては、流動のプラントル数依存性、数がきわめて大きくなった究極の乱流状態、速度・温度境界層の振る舞い、プリュームの発生と合体、など興味ある課題が多数ある。境界層、噴流や混合層などで議論されてきた秩序構造と、熱乱流中の巨視的流動は大きく異なる。しかし、両者を結び付ける接点は乱流を理解するうえで、何らかの指標を与えてくれるものと予想している。

本研究は、益子岳史氏（静岡大学）、佐野雅己氏（東大）との共同研究として行われました。また、実験に協力してくれた水野孝俊君、早川智博君に感謝いたします。