
北海道大学大学院 工学研究科
Center for Nonlinear Dynamics, The University of Manchester
Yuji.Tasaka@manchester.ac.uk
| TED Plaza |
| 非線形現象と熱流体工学 |
| 内部発熱流体層における対流パターン形成 |
 |
田坂 裕司 北海道大学大学院 工学研究科 Center for Nonlinear Dynamics, The University of Manchester Yuji.Tasaka@manchester.ac.uk |
 |
 |
 |
 |
| 柳澤 孝寿 海洋研究開発機構 地球内部変動研究センター |
高橋 潤平 北海道大学大学院 工学研究科 |
村井 祐一 北海道大学大学院 工学研究科 |
武田 靖 北海道大学大学院 工学研究科 |
|
1. はじめに
暖かい味噌汁をお椀に注ぎしばらく待つと,表面での冷却により生じた流れが作り出す,綺麗な対流パターンを観察することができる.これは自然対流によるパターン形成の例として,多くの方が説明に用いられているのではないだろうか.著者は学生に紹介する際,お椀をゆっくり回してさらに回転の効果を加えてみることを勧めている.食堂で学生がこぞってお椀を回しているところを想像すると異様に思えるが,絶妙な回転数が実現できれば味噌汁が冷めるまでにさらなる流れのパターンを観察することができる.これらの流れのパターンはそれぞれ,流体の温度差による浮力と粘性,あるいは表面張力,遠心力,コリオリ力などがバランスした結果として生じる.これらは見て楽しいだけではなく,熱流体物理学あるいは熱流体工学における基礎的な現象であることは周知のことであろう.よって,流れが作り出すパターンの背後にある物理,非線形作用などを理解することは,それらの発展にとって非常に重要である. 水平層内に生じる自然対流の問題は,Bénardにより初めて系統的な研究が行われ, Rayleighによる安定性解析など理論的な背景が構築された.その後,乱流に至る遷移過程からカオス的な振る舞いが見いだされ,近年でも乱流遷移の例として,あるいは乱流遷移の普遍的な過程を見いだすための対象として,盛んに研究が行われている.一方,1960年代後半からそれと平行して,外部からの加熱ではなく,流体自身が発熱することによって生じる自然対流現象に関する研究が行われてきた[1,2].これらは主に,原子力工学や天体規模の流動現象をその研究背景としている.一例を挙げると,地球内部のマントルは種々の岩石によって構成されているが,地球物理学では極高粘性の流動体として扱われる.また岩石に含まれる放射性元素の崩壊が熱源となり,熱対流(マントル対流)が生じている.地球物理学における内部発熱現象の取り扱いは,地球物理学の専門書[3]を示してここでは割愛する.本報ではそのような内部発熱により駆動される流体層に形成される,対流パターンについて紹介する. 2. 系の設定,実験装置ならびに方法Rayleigh-Bénard対流と同様に,厚さLの水平流体層を考える.境界条件として,層の上面を等温冷却面,下面を断熱面とする.流れ場の支配パラメータとして,熱伝導時における上面と下面との温度差を代表温度として用いることにより, 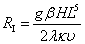 のようにレイリー数(内部レイリー数)が定義される.ここで,式中のg,β,H,λ,κおよびνはそれぞれ,重力加速度,流体の体積膨張率,単位時間・単位体積あたりの内部発熱量,流体の熱伝導率,温度伝導率ならびに動粘性係数である.線形安定論に基づいて見積もられた対流の生じる臨界レイリー数は,Rc = 1386である[4].またこれまでの実験により,対流は超臨界で生じることが確認されている.実験パラメータとして,R* = RI / Rcを定義し,以後これを用いて実験結果を整理する. 実験装置の略図を図1に示す.水平流体層を想定し,水平方向は流体層高さLの30倍の長さとした.熱源を内部発熱のみに制限するため,流体層下面に真空断熱ガラスを設置し,下面を断熱条件とした.上面には熱伝導率の高いアルミニウム板を用い,その上に冷却水を循環させることにより等温冷却面とした.流体層に接する面は,酸化膜の形成と黒色塗料の塗布により電気的絶縁を施した.流体層の両側に電極を設置し,作動流体である0.5 wt% KCl水溶液に電流を流すことにより生じるジュール熱を,時空間に対して一様な内部発熱源とした.作動流体中に板状微粒子を混入し,流れ場の可視化を行った.種々のレイリー数RIについて,可視化された流れ場を流体層下面から撮影した.  図1 実験装置概略図 3. 対流パターンとその遷移 R* = 4で撮影されたセルパターンを図2左に示す[6].形成されたセルは,いびつであるがいずれも六角形であり,また中心は下降流となっている.Rayleigh-Bénard対流の安定性解析[5]によると,熱伝導状態における温度分布が理想的な線形分布の場合,同方向に回転軸を持つ二次元ロール群が安定となるが,温度分布が上に膨らむように僅かにずれた場合,このような下降流を持つ六角形セルになることが知られている.この系における温度分布の熱伝導解は上に凸の放物型であり,よってこの可視化結果は安定性解析の結果と比べて妥当である. 六角形セルは,図のようにレイリー数の増加と共に膨張し,最終的には発生直後に比べ,長さスケールで二倍程度まで拡大する.Rayleigh-Bénard対流では,レイリー数がある程度の値になると,流体層全体に誘起される浮力よりもむしろ,上下の等温面に形成される温度境界層のはく離が支配的となる.一方内部発熱対流では,下面には温度境界層が形成されないため,専らはく離した上面の温度境界層の沈み込みにより対流運動が駆動されており,低いレイリー数では下面近傍の対流運動が活発ではないと予想される.よってこのようなセルの拡大は,上面温度境界層のはく離により持ち込まれる運動量が大きくなり,対流が流体層全体に及ぶためであると考えられる.  図2 各レイリー数における対流セルパターンの可視化写真,写真右上の四角は大きさの指標で一辺が2L R* = 10を越えると,拡大したセルは異なる構造へと遷移する.図3(a)と図3(b)はR* = 10で撮影された同じ一枚の可視化写真から切り出したものである.図3(a)では,拡大したセルの中にもう一つのセルが形成されている.一方図3(b)では,セルの中心から外周に向かってスポーク状の下降流が形成されている.図4に,R* < 10で観察される六角形セルを含めた各対流セル構造における流れの特徴を示す. 二重セル構造(図4(b))では,セルの中心は上昇流となり,それを取り巻くように下降流領域が存在し小さなセルを形成する.スポーク状の構造(図4(c))では,それまで同心円状に拡大した下降流領域が変形し,いびつな形状を取っている.スポーク状の構造は,上面温度境界層の大規模なはく離と下面から押し戻された暖かい上昇流との干渉が原因であると考えられるが,二重セル構造が形成される要因,またこれらの構造が混在する原因は明らかでない.数値計算結果[7]では,図3(c)に示すようにスポーク状の構造が定常状態として現れており,この構造が六角形セルの通常分岐として生じることが確認できる.また数値計算によると,レイリー数の増加とともにスポーク状の構造ではその下降流領域がさらに拡大し,最終的には隣接するセルの下降流領域と結合して大規模な沈み込み帯を形成する.  図3 新たに生じた対流セル構造:(a)二重セル構造,(b)スポーク状構造,(c)数値計算で確認されたスポーク状構造  図4 各対流セル構造における流れの特徴:(a)六角形セル,(b)二重セル構造,(c)スポーク状構造 二重セル構造が形成される過程を定量的に調べるため,PIVにより水平面の二次元速度ベクトル場を計測した結果を図5に示す[8].図5(a)はその一例であり,流体層の下面近傍を計測したことから,流れはセル中心から外側に向かっている.図5(b)-(f)は,まずR* ~ 6において定常な六角形セルを形成させ,その状態からレイリー数を上昇させてR* ~ 14とし,時間経過に対するセル形状の変化を調べた物である.粒子画像の撮影はレイリー数上昇後2~5分間隔で行った.一度の計測で6枚の画像を速度ベクトル場の導出に用いて,その結果から時間平均を求めた.さらに,連続の式から数値積分により鉛直方向速度を算出した.図5(b)から(f)までそれぞれ順に,レイリー数を上昇させてから0,6,12,24,60分後の流れ場の様子を示す.なお図中の色は,それぞれ赤が上昇流を,青が下降流を示している.また色の濃さが速度の大きさを表している. 図5(b)と図5(c)との比較から分かるように,速度の増加はレイリー数増加から6分程度で終了し,その後セルの拡大が始まっている.また図から分かるように,速度の増加はセル中心の下降流において顕著である.個々のセル拡大に伴いセル同士の結合が生じる(図5(d)).セルの肥大化はそれ自身の拡大,あるいはセル同士の結合により時間経過とともにさらに進行し,図5(e)で示す段階では異なるサイズのセルが混在している.また一部のセルにおいてスポーク状の下降流が形成され始めていることがわかる.時間が十分経過した図5(f)においては,セルの拡大はほぼ終了し,セルサイズは流体層内でほぼ一定となっている.また図の中心付近において,セル同士の結合により中心に上昇流域を挟んだ状態で安定化に向かうセルが確認できる.このようなセルは流体層全体に現れるわけではなく,一部のセルを除いてはスポーク状の下降流を持つセルに遷移する.このことから,二重セル構造が形成される条件として,セルの成長段階において水平方向の領域制限や温度分布形成による非一様内部発熱など,理想的な系では生じない不確定な要素が加わることが考えられる.  図5 (a)PIVにより計測された対流セルの速度ベクトル場,(b)-(f)時間経過に伴う速度場の変化.色は赤が上昇流を,青が下降流をそれぞれ示している. 4. おわりに 対流現象に現れるパターン形成の例として内部発熱による自然対流を取り上げ,可視化写真を中心に対流セルパターンの遷移を解説した.低いレイリー数では,中心が下降流となる六角形セルが形成されること,レイリー数の増加と共にセルが拡大すること,その後,スポーク状構造または二重セルの構造に遷移することを示した.スポーク状構造は数値計算からも示されており,流れの通常分岐の結果として生じることが確認できた.しかしながら,二重セル構造は実験以外では確認されておらず,流れ場全体を考慮した流れの安定性解析などにより,この状態が一つの安定解であることを理論的に示す必要がある.このような実験による新たな現象の発見が,広い分野での発展に繋がると考えている. 参考文献[1] Tritton, D. J. & Zarraga, N. M. J. Fluid Mech., 30(1967), pp. 21-32. [2] Schwiderski, E. W. & Schwab, H. J. A., J. Fluid Mech., 48 (1971), pp. 703-719. [3] Turcotte, D. L., et al. "Geodynamics 2nd edition", Cambridge Univ. Press, (2001). [4] Roberts, P. H., J. Fluid Mech., 30 (1967), pp.33-49. [5] 吉崎正憲,流体力学ハンドブック第2版,(1998),pp.722-732. [6] Tasaka, Y., et al., J Visualization, 11 (2008), pp. 213-220. [7] Ichikawa, H., et al., Phys. Fluids,18 (2006), 038101.[8] 高橋ら,日本流体力学会年会2008講演要旨集,pp.61,拡張要旨集CD-ROM#12013,(2008) |