3. 計算力学
3.1 はじめに
3.2 計算固体力学
3.3 計算流体力学
3.4 大規模解析計算
3.4.1 スーパーコンピュータ「富岳」/3.4.2 飛沫・エアロゾルの飛散シミュレーション/3.4.3 ゴードン・ベル賞
3.5 マルチスケール(マテリアル関係)
3.5.1 金属材料/3.5.2 複合材料/3.5.3 高分子材料・ソフトマテリアル
3.6 計算バイオメカニクス
3.7 逆問題・データ同化・最適化
3.8 機械学習と計算力学の融合
3.9 産業界での計算力学
3.10 防災関連
3.1 はじめに
2020年度は,人類にとって特別な年となった.COVID-19の影響により,国際連携を中心に学術的活動に関しても改めて多くのことを考えさせられる1年となった.緊急事態宣言等により,実験室での実験にも影響が生じ,在宅でも実施可能なシミュレーション寄りの研究テーマがこれまでとは違った理由で重要な意味を持つこととなった.コロナとは直接関係なく,最近の研究のトレンドは,やはりデータ駆動型の研究であろう.機械学習,深層学習,データ同化,ビッグデータ,デジタルツインなどをキーワードに,計算力学分野で従来行われて来た,力学の基礎方程式を数値計算により解析する研究に加え,情報科学の分野と融合し,今後,どのような発展を遂げていくのか様々な議論が行われている.この年鑑でも関連する研究が多く紹介されている.また,計算機科学の分野では,スパコン「富岳」が計算速度世界一を2020年6月に達成し,2021年の7月の段階で3期にわたり世界最高の性能を維持している.COVID-19に関連した数値解析なども行われ,数値計算結果が感染拡大防止などに利用されている.今後は,カーボンニュートラルなども重要なキーワードとなり,この分野のますますの発展と社会への大きな貢献が期待されている.
〔高木 周 東京大学〕
3.2 計算固体力学
2020年はCOVID-19の感染が急速に拡大し,その被害が世界中に広がる記録的な一年であった.計算固体力学分野では,国内の主要な研究交流の場である計算力学講演会(第33回・鹿児島大学)が開催中止となり(1),4年に1度開かれる理論応用力学国際会議(ICTAM・イタリア)もまた1年間の開催延期へと追い込まれた(2).2020年の上半期は先の見えない状況が続いたが,そうした中でも一部の研究会(学際大規模情報基盤共同利用・共同研究拠点シンポジウムなど)では,従来の対面開催からオンライン開催への切り替えが図られた.オンライン開催の是非については賛否両論挙げられているが,結果的には2020年の下半期には多くの学会・研究会がオンラインで開催され,停滞した研究交流がようやく息を吹き返した.このように,2020年はCOVID-19により研究交流が大きな制限を受けたことから,ここで年内の研究動向を網羅的に紹介するのは難しい.そのため,本節では計算固体力学分野において注目されつつあるトレンドとして(i)連続体力学理論の一般化,および(ii)情報科学の導入の二つを取り上げ,それらの研究動向について紹介したい.
一般に,固体材料の内部で生じる力学現象は広範な時空間上に広がっている.そのため,計算固体力学では解析対象に応じて用いる基礎理論が異なっている.これを大別すると,電子系を取り扱う量子力学,原子・分子レベルの離散系を対象とするニュートン力学,マクロ系を解析する連続体力学である.これらの基礎理論に対する代表的な計算方法は,それぞれ第一原理計算,分子動力学計算,およびフェーズフィールド法・有限要素法である.折しも,2020年は最新鋭のスーパーコンピュータ「富岳」が運用を開始したことから,これを追い風として,計算固体力学は今後も大きく発展し続けることが期待されている.しかしながら,マシンパワーのみを頼りにした力学現象の解析にはおのずと限界があるため,力学解析のための新しい方法論の模索が続けられてきた.これらの方法論をマルチスケールという視点から捉えると,二つの大きなトレンドが見えてくる.一つは連続体力学理論の一般化であり,もう一つは情報科学の導入である.前者に関する代表的な取り組みとしては,一般化連続体力学の導入が挙げられる.この理論の特徴は,連続体の構成要素(連続体粒子)を併進運動のみが許された質点とみなすのではなく,それ自身が変形・回転の自由度を備えた変形素子と捉える点にある.この際に導入される変形素子の大きさが理論を非局所化し,解析結果にサイズ効果を生み出す.具体的には,ひずみ勾配結晶塑性理論や,均質化法による周期構造体の力学特性解析などが挙げられる.連続体力学の一般化に関するもう一つの取り組みとして,微分幾何学の導入が挙げられる.通常,連続体力学はユークリッド空間上で構成されているが,これをリーマン計量と接続を備えた抽象的な空間(リーマン・カルタン多様体)へ拡張することによって,弾性変形と塑性変形の乗算分解が自然に実現される.これを特性長さの含まれた境界値問題として定式化すると,マルチスケール解析が実現される.一方,情報科学の導入に関しては,ニューラルネットワーク・機械学習が中心的な役割を果たしている.ミクロスケールの計算固体力学では,機械学習は原子間に働く相互作用ポテンシャルの開発に用いられている.第一原理計算結果と機械学習を組み合わせてニューラルネットワークポテンシャルを構築し,これを分子動力学計算へ実装することによって,量子力学に基づく高い解析精度を持った動力学計算を実現させる試みである.また,分子動力学法とフェーズフィールド法という二つの異なる解析法を接続したトランススケール解析も検討されている.ここでは,アンサンブルカルマンフィルタを用いた材料特性の推定とデータ同化が用いられている.一方,マクロスケールの取り組みとしては,Physics-Informed Neural Networks(PI-NN)の応用が進められている(3).これはニューラルネットワークを構築する際に,学習データが従う支配方程式の情報を積極的に利用するもので,学習効率の大幅な改善が期待されている.国内での研究報告は見られないものの,海外では既にPI-NNと画像解析で大きな成功を収めたGenerative Adversarial Networks(4)の融合について検討が進んでいる.スケールごとに使用法の差が見られるものの,情報科学への期待が新しい研究のトレンドを形成しつつある.
〔垂水 竜一 大阪大学〕
参考文献
(1) https://www.jsme.or.jp/cmd/conference/cmdconf20/
(2) https://www.ictam2020.org/
(3) M. Raissi, P. Perdikaris, and G. Karniadakis. Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial dierential equations. J. Comput. Phys., 378, pp. 686-707 (2019).
(4) Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville, and Yoshua Bengio, Generative adversarial nets, Advances in neural information processing systems, pp. 2672-2680 (2014).
3.3 計算流体力学
新型コロナウイルス(COVID-19)の蔓延による緊急事態宣言の発出やこれに伴うイベント開催自粛等により,本会主催の2020年度第33回計算力学講演会(1)は中止となった.また,本会が協賛する日本計算工学会主催第25回計算工学講演会(2)も中止を余儀なくされた.さらに,本会が日本計算力学連合(JACM)を介して協力する国際計算力学連合(IACM)主催14th World Congress on Computational Mechanics(WCCM)(3)も2021年1月に延期され,オンラインでのバーチャル会議として開催された.WCCMは,特定課題を対象としたミニシンポジウムから構成されるが,コロナ禍のバーチャル会議のため講演取りやめ等が散見されたことから,この会議から全体的な動向を把握することは非常に困難である.その他,International Congress on Theoretical and Applied Mechanics (ICTAM)(4),International Symposium on Turbulence, Heat and Mass Transfer (THMT)(5)等の国際会議の多くも延期となった.米国物理学会(APS)主催のDFD Meeting(6)はバーチャル会議として開催されたが,コロナ禍での開催のため,その内容が本年度の動向を正確に反映しているかどうかの判断は難しい.このような状況の中,例年通りの規模で開催された計算流体力学関係の会議は,オンライン開催ではあるが,日本流体力学会主催(本会協賛)の第34回数値流体力学シンポジウム(7)だけであった.
コロナ禍により,研究活動は一様に停滞したと予測されるが,理化学研究所・神戸大学の坪倉誠教授を中心とする飛沫感染シミュレーションがマスコミ・メディアから注目を浴びることとなり,計算流体力学の有効性や意義を社会に示すこととなった.2020年度から試験運用が開始された「富岳」がこのシミュレーションに用いられていたことも大きな注目を浴びる要因の一つであったと推察される.このような新型コロナウイルス感染拡大防止に関連する一連の解析により,計算流体力学が社会的に認知されるようになったことは,年鑑として特筆すべき事項と思われる.
前述のように,この分野で唯一従来通りの規模で開催されたのは第34回数値流体力学シンポジウムであった.規模が維持できたのは,開催予定が12月であったこと,2020年度に予定されていた東京オリンピック・パラリンピックの余波を考慮に入れて開催地を東京から沖縄に当初から移されていたこと,12月にはコロナ禍を脱しているとの期待感があったこと等によるものであり,最終的に250件近い研究発表が行われ,参加者も500名を超えた.なお,坪倉誠教授(理研・神戸大学)による「富岳による新型コロナ飛沫・エアロゾル感染シミュレーション」と題した特別講演が企画されたことも多くの参加者を集める要因となったと思われる.この分野の国内動向を把握するために,2020年度の年鑑(8)においても数値流体力学シンポジウムの講演データが採用されている.ここでは,2019年度のデータに2020年度のデータを追加する形で,それぞれの研究分野の動向を分析する.表1は,数値流体力学シンポジウムにて企画された各OSの発表件数の推移を示している.2019年度の年鑑データ(8)に2020年度のデータ(7)を追加するとともに,2016年から2019年までの平均値とそれに対する2020年の増減率も追加情報として含めた.なお,表中のOSの並びは増減率順である.最も特異な推移を示しているのは「可視化,データ同化,機械学習」に関する講演数であり,2020年度は2016年から2019年の平均値に対して倍増,2016年比で5倍程度まで増加している.新たな解析方法としてデータ同化と機械学習が近年注目されていることから,この増加傾向は今後も数年は維持されると予測される.次に大きく増加している分野は「原子・分子の流れ」であり,2020年度に急激に増加している.この要因は定かではないが,分子動力学計算に関する計算技術が成熟し,「京」「富岳」を含めて全国のスーパーコンピュータに汎用のソフトウェアが整備されてきたことと関係する可能性がある.「新規解法及び高性能化に向けた既存手法改良」についても増加傾向にあるが,これには「富岳」の稼働が関係している可能性がある.「混相流体,相変化,反応,界面」と「乱流,渦,波動」についても増加が認められるが,従来から研究発表が多い分野であるため,発表件数の全体的な増加に伴う変動の範囲内とも考えられる.「種々の連成問題」,「複雑流体の流れ」及び「エネルギーに関連する流れ」についてはほぼ例年通りであり,大きな変化は観察されない.比較的講演件数の減少幅が大きな分野は,「輸送用機械に関連する流れ」,「地域環境と防災」及び「連続体力学的解法」である.このうち,「輸送用機械に関連する流れ」については年度変動の範囲内にあるようにも感じられるが,「地域環境と防災」と「連続体力学的解法」については明らかな減少傾向が観察される.「地域環境と防災」では,局地豪雨の短期予測が実用化される等,ある程度の成果が生み出されたためとも考えられる.「連続体力学的解法」についても同様であり,この分野の技術が成熟したためとも解釈できる.大幅に講演数が減少した分野は,「離散要素型解法」と「非圧縮流れ解法,圧縮流れ解法」であり,「連続体力学的解法」と同様にどちらの分野も成熟の域に達した可能性がある.なお,規模的には例年以上に達した第34回数値流体力学シンポジウムであったが,コロナ禍により発表を控えた研究グループも存在したことから,上述の動向にコロナ禍の影響が含まれており,特定の分野の研究発表が極端に減少した可能性があることは否定しない.
機械学習やデータ同化に関連した分野のように,数値として明確な傾向は観察されないが,新型コロナ感染症の感染拡大防止に関わる研究報告が新たに加わっている.それらは,鉄道車両や室内の換気に関するものであり,「輸送用機械に関連する流れ」と「地域環境と防災」に含まれている.上述のように両分野は講演件数を減らしているように見えるが,この種の研究はWith/Postコロナ時代にも必要とされるものであり,今後研究発表が増加する可能性がある.また,「大規模・高速計算,新しい計算資源の利用」についても,講演件数を大きく減らしているように見えるが,これは「京」から「富岳」への過渡期であったためと思われ,「富岳」の一般運用が開始される2021年以降は増加が期待できる(表3-3-1).
表3-3-1 数値流体力学シンポジウムにおける講演件数の推移
| OS名 | 2016 | 2017 | 2018 | 2019 | 平均 | 2020 | 増減率 |
| 可視化,データ同化,機械学習 | 6 | 12 | 18 | 19 | 13.75 | 27 | 96.4% |
| 原子・分子の流れ | 10 | 4 | 15 | 13 | 10.50 | 20 | 90.5% |
| 新規解法及び高性能化に向けた既存手法改良 | 6 | 12 | 9 | 6 | 8.25 | 13 | 57.6% |
| 混相流体,相変化,反応,界面 | 15 | 14 | 17 | 19 | 16.25 | 24 | 47.7% |
| 乱流,渦,波動 | 25 | 28 | 30 | 25 | 27.00 | 37 | 37.0% |
| 種々の連成問題 | 15 | 15 | 21 | 15 | 16.50 | 17 | 3.0% |
| 複雑流体の流れ | 12 | 15 | 19 | 20 | 16.50 | 16 | -3.0% |
| エネルギーに関連する流れ | 16 | 11 | 11 | 14 | 13.00 | 12 | -7.7% |
| 輸送用機械に関連する流れ | 27 | 12 | 21 | 22 | 20.50 | 17 | -17.1% |
| 直交細分化・適合細分化格子法 | – | – | – | 10 | 10.00 | 8 | -20.0% |
| 地域環境と防災 | 30 | 28 | 23 | 22 | 25.75 | 19 | -26.2% |
| 一般セッション | 11 | 3 | 0 | 9 | 5.75 | 4 | -30.4% |
| 連続体力学的解法 | 15 | 19 | 22 | 10 | 16.50 | 11 | -33.3% |
| 電磁流体,プラズマ流 | 4 | 7 | 10 | 7 | 7.00 | 4 | -42.9% |
| 大規模・高速計算,新しい計算資源の利用 | 8 | 11 | 5 | – | 8.00 | 4 | -50.0% |
| 設計探査,最適化 | – | – | – | 4 | 4.00 | 2 | -50.0% |
| 離散要素型解法 | 16 | 23 | 22 | 18 | 19.75 | 9 | -54.4% |
| 非圧縮流れ解法,圧縮流れ解法 | 11 | 16 | 17 | 6 | 12.50 | 5 | -60.0% |
〔店橋 護 東京工業大学〕
参考文献
(1) https://www.jsme.or.jp/cmd/conference/cmdconf20/index.html (参照日2021年6月25日)
(2) https://www.jsces.org/koenkai/25/ (参照日2021年6月25日)
(3) https://virtual.wccm-eccomas2020.org/ (参照日2021年6月25日)
(4) https://www.ictam2020.org/ (参照日2021年6月25日)
(5) http://www.thmt-21.org/ (参照日2021年6月25日)
(6) http://meetings.aps.org/Meeting/DFD20/APS_epitome (参照日2021年6月25日)
(7) https://www2.nagare.or.jp/cfd/cfd34/index.html (参照日2021年6月25日)
(8) https://www.jsme.or.jp/kikainenkan2020/chap02/#a03 (参照日2021年6月25日)
3.4 大規模解析
2020年度の高性能計算分野における最も大きな話題は,スーパーコンピュータ「富岳」が完成し運用が開始されたことだと思うが,新型コロナウイルスの影響で「富岳」の話題が薄れてしまった印象もある.一方で,「富岳」を用いた新型コロナウイルス対策研究の成果が多くメディアに取り上げられ,スパコン利用の有用性がこれまでになく世間に注目された年だったようにも感じる.
3.4.1 スーパーコンピュータ「富岳」
2012年から稼働していた「京」コンピュータは,2019年8月30日にシャットダウンされ,その役目を終えた.「富岳」は,「京」の後継機として2014年3月に理化学研究所から開発が発表され,2019年4月に富士通が製造を開始,同年5月に名称が「富岳」と決定され,同年12月から「京」コンピュータがあった神戸市ポートアイランドの理化学研究所計算科学研究センターに設置が始まった(1).スーパーコンピュータ(スパコン)の性能ランキングは毎年2回,6月にドイツで開催されるISC (International Supercomputing Conference)と11月にアメリカで開催されるSC (Supercomputing Conference)において発表される.「富岳」は,2020年5月末において全てのシステム設置が完了していなかったが,6月のスパコン性能ランキングにおいて,TOP500,HPCG,Graph500,HPL-AIの4部門において第1位となった.全システムが完成した後の11月のランキングでも同4部門で1位となり,2020年は2回連続の4冠となった.「富岳」はその開発時にシステムとアプリケーションを協調設計するCo-Designが行われ,汎用CPUのみを使ってアプリケーションの高い性能を引き出すことを重視した.また,9つのポスト「京」研究開発枠重点課題,「富岳」成果創出加速プログラム等が先行して進んでいたため,2021年3月の「富岳」の正式運用開始より先に成果が出ている.「富岳」の開発時の詳細な話は書籍(1)(2)で述べられている.
「富岳」は432台のラックから構成され,各ラックには192枚のボード,各ボードには2個のCPU(富士通A64FX),各CPUに1ノード,各ノードは48コアを有し,「富岳」全体としては158,976ノード(CPU),7,630,848コアから構成されている(計算が合わないのは,432ラックのうち36ラックが192ノード構成のためである)(3).ここでは「富岳」とGPUスパコンの簡単な比較を行ってみる.「富岳」の1ノードの演算性能は3.1 Tflops,メモリ帯域幅は1,024 GB/sであり,B/F (Byte/Flop)値は0.33である.NVIDIA A100 GPUは,演算性能は9.7 Tflops,バンド幅は1,555 GB/sであり,B/F値は0.16である.一般的なGPUスパコンの1ノードは4 GPUであることを考えると,1ノード当たりの演算性能は38.8 Tflopsとなり,「富岳」の12.6倍となる.一方,「富岳」のB/F値はGPUの2.1倍あり実行性能が出やすいといえる.演算性能とB/F値を考えると,A100を用いたGPUスパコンの方が1ノード当たり約6倍高性能と考えることができる.GPUスパコンのノード数を1,000とすると,約16万ノードの「富岳」の性能はGPUスパコンの約27倍となりその凄さを伺い知ることができる.
3.4.2 飛沫・エアロゾルの飛散シミュレーション
テレビの番組でコンピュータシミュレーション結果が示されることはあるが,一般の人がそれを身近に感じることはあまりなかったように感じる.2020年はコンピュータシミュレーションが一般の人々に大変身近になった年ではないだろうか.連日のように飛散シミュレーションの動画がテレビで紹介され,普段は見えないエアロゾルの運動が可視化され,ソーシャルディスタンス,マスクの着用方法,フェースマスクの有効性など,日常生活のコロナ対策にシミュレーション結果が活かされた.理化学研究所の坪倉らのグループは(4),京都工芸繊維大学の山川らのモデル(5)を基本とした飛沫シミュレーションを「富岳」上で行い,その第一弾の成果を2020年6月3日に報告している(6).第1回目の緊急事態宣言が出されたのが4月7日なので,わずか2か月程度ではじめの成果に達したことになる.担当した研究者のスパコン利用のノウハウと努力に加え,「富岳」を用いたことで絶対的計算速度の向上,時空間スケールと解像度の飛躍的向上,ケーススタディーの容易性,さらに「富岳」で用いられているCPUが汎用性の高いものであることなどが早期の成果に繋がった理由であると考えられる.「富岳」のCo-Designの成果が現れたともいえる.
3.4.3 ゴードン・ベル賞
高性能計算の分野において最も権威のあるゴードン・ベル賞は,毎年国際会議SCで発表される.2020年のSC20はオンラインで開催され,6件のファイナリストのうち1件が受賞した.「富岳」を用いた日本の研究は,2件がファイナリストに選出された(7)(8).ゴードン・ベル賞を受賞した論文は「Pushing the limit of molecular dynamics with ab initio accuracy to 100 million atoms with machine learning」(9)であり,機械学習に基づく第一原理計算Deep Potential Molecular Dynamicsによって1億原子1 nsの計算を1日で達成した.また,SC20においては,新型コロナウイルスに関する研究の賞が設けられ,「AI-Driven Multiscale Simulations Illuminate Mechanisms of SARS-CoV-2 Spike Dynamics」(10)が受賞した.上記の2件の受賞研究は,アメリカのオークリッジ国立研究所のスパコンSummitにおいて行われた.
〔高木 知弘 京都工芸繊維大学〕
参考文献
(1) 日経クロステック編集, 富岳 世界4冠スパコンが日本を救う(圧倒的1位に輝いた国産技術の神髄) (2021).
(2) 小林雅一, 「スパコン富岳」後の日本 科学技術立国は復活できるか (2021).
(3) スーパーコンピュータ「富岳」資料,富士通 https://www.fujitsu.com/jp/about/businesspolicy/tech/fugaku/specifications/ (参照日2021年4月12日)
(4) 坪倉誠,「富岳」で飛沫感染防止に貢献する, 『理研ニュース』2020年11月号 特集.
(5) Yamakawa, M., Kitagawa, A., Ogura, K., Chung, Y.M., Kim, M., Computational investigation of prolonged airborne dispersion of novel coronavirus-laden droplets, Journal of Aerosol Science, Vol. 155, (2021), 10.1016/j.jaerosci.2021.105769.
(6) 室内環境におけるウイルス飛沫感染の予測とその対策(課題代表者;理化学研究所/神戸大学 坪倉 誠), 理化学研究所計算科学研究センター https://www.r-ccs.riken.jp/fugaku/history/corona/projects/tsubokura/ (参照日2021年4月12日)
(7) Yashiro, H. et al., A 1024-member ensemble data assimilation with 3.5-km mesh global weather simulations, Proceedings of SC20 (2020), 10.1109/SC41405.2020.00005.
(8) Kato, C.et al., Toward realization of numerical towing-tank tests by wall-resolved large eddy simulation based on 32 billion grid finite-element computation, Proceedings of SC20 (2020), 10.1109/SC41405.2020.00007.
(9) Jia, W. et al., Pushing the limit of molecular dynamics with ab initio accuracy to 100 million atoms with machine learning, Proceedings of SC20 (2020), 10.1109/SC41405.2020.00009.
(10) Casalino, L.et al., AI-Driven Multiscale Simulations Illuminate Mechanisms of SARS-CoV-2 Spike Dynamics, bioRxiv (2020), 10.1101/2020.11.19.390187.
3.5 マルチスケール(マテリアル関係)
種々の機械材料は,着目するスケールによって大きく様相が異なる階層構造,いわゆるマルチスケール構造を有している.微視的スケールの材料挙動が,巨視的な材料の機械特性に大きな影響を及ぼすと考えられることから,個々のスケールの材料挙動に着目した実験的,理論的研究はもちろんのこと,複数のスケールを横断したマルチスケール材料モデリングやシミュレーション手法の開発が精力的に進められている.実験観察の技術革新と知見の拡大や,計算機性能の向上から,マルチスケール解析の適用範囲や解析精度は大きな進歩を遂げているが,依然として未解明の現象やモデル化に困難を伴う材料挙動も多い.
2020年は新型コロナウイルス感染症の影響により,従来の研究報告の場の多くが中止やオンライン開催となった.計算力学部門が主催する第33回計算力学講演会(CMD2020)も中止を余儀なくされたが,部門主導の研究発表の場としてCMD2020計力スクウェアがオンライン企画として開催され,マルチスケール解析に関連する研究も複数の報告がなされた(1).また,計算力学分野において最大規模の国際会議である14th World Congress in Computational Mechanics (WCCM2020)が,ECCOMAS Congress 2020と併催された(2).本会議は,本来は2020年7月にフランス・パリで開催予定だったが,最終的に2021年1月にオンラインでの開催となったものである.オンライン開催とはなったものの,WCCM2020においても多数のマルチスケール関連のMinisymposiaが企画されており,当該分野に対する代わらぬ関心と研究のアクティビティの高さが伺えた.
本節では,日本機械学会論文集掲載論文や,CMD2020計力スクウェア,WCCM2020での講演を中心に,マテリアル関連のマルチスケール解析について,最新の研究動向を概説したい.
3.5.1 金属材料
金属材料は,機械材料として現在まで最も広く利用されており,マルチスケール解析に関する研究報告の数は2020年現在においても非常に多い.結晶塑性モデルによるメゾスケールシミュレーション(3)(4),分子動力学法による原子スケールシミュレーション(5),Muli-phase-fieldモデルと転位-結晶塑性モデルを用いた動的再結晶シミュレーション(6)など,多様なスケールを考慮した研究がなされている.また,Weitzenböck多様体によるらせん転位の新たなモデル化を行った報告もある(7).CMD2020計力スクウェアにおいては,5章からなる研究報告集の第4章が金属材料に関する研究報告に充てられており,マルチスケールの視点からの研究も複数報告されている(1).WCCM2020でも,金属材料を対象としたマルチスケールモデリングに関する講演は多く,巨視的スケールから原子・電子スケールまでの多様なスケールでのモデリングの精緻化はもちろん,各スケールを橋渡しするための数値計算手法についても,多様なアプローチが展開された.
3.5.2 複合材料
微視的内部構造を有する複合材料は,従前よりマルチスケールモデリングの対象として幅広い研究がなされてきた.近年は,内部構造の不確かさを考慮したマルチスケールシミュレーションが盛んに行われている.例えば,内部構造の不確かさが複合材料のミクロ損傷とマクロ強度に及ぼす影響や,積層造形品の造形不良が力学的特性に及ぼす影響を評価する試みが,より小さなスケールに着目した研究としては,分子動力学法を用いた金属とポリイミド分子の複合構造に関する評価などが報告されている(1).また,メゾスケールモデルによるズーミング解析によって,CFRP製圧力容器の高精度な強度評価を行った研究(8)や,均質化理論を用いたCFRPの損傷解析(9)も報告されている.WCCM2020においても,複合材料に関連する複数のMinisymposiaが企画され,均質化理論に基づく種々の定式化やreduced orderモデリング,微視的損傷のモデリング,確率論的モデリングなど,様々なアプローチによる複合材料のマルチスケールシミュレーションについて,議論がなされた.
3.5.3 高分子材料・ソフトマテリアル
樹脂材料やエラストマーなどの高分子材料,ソフトマテリアルも,マルチスケールモデリングの対象として,近年大きな発展の見られる分野である.高分子材料のマルチスケール構造は金属のそれと大きく異なるため,金属に対して提案されてきた従来の手法やモデル化では不十分な場合も多く,高分子材料に特化したモデリング,解析手法の構築がなされている.ミルフィーユ構造と呼ばれる微視的積層構造を有した高分子材料の挙動を,場の理論によって解析した研究(1),膨潤エラストマーの材料挙動を超弾性モデルで表現し,汎用有限要素解析ソフトウェアに実装した研究(10),熱硬化性樹脂の硬化反応モデリング(11)などが報告されている.WCCM2020では,粘弾性や超弾性を考慮した一般的な高分子材料のモデリングに加え,熱力学的連成を考慮した樹脂材料のモデリングやPhase-field法,分子動力学法などを活用したモデリングなど,いわゆるマルチフィジクスを考慮したアプローチも多く見られた.高分子材料やソフトマテリアルは,マルチスケールモデリングの対象として,今後ますます精力的な研究が進められる分野であると思われる.
〔只野 裕一 佐賀大学〕
参考文献
(1) CMD2020計力スクウェア研究報告集(2020)
https://www.jsme.or.jp/cmd/japanese/events/2020/cmd2020_report.pdf(参照日2021年4月1日)
(2) 14th WCCM & ECCOMAS Congress 2020: Book of Abstract(2021)
http://r.cnam.fr/wccm-eccomas-book-of-abstracts(参照日2021年4月1日)
(3) 佐藤満弘, 大橋鉄也, 河野義樹, 半導体素子の生産過程で蓄積する転位の抑制に関する結晶塑性解析, 日本機械学会論文集, Vol. 86, No. 884 (2020),transjsme.19-00457.
(4) Yuichi Kimura, Ryo Ueta, Kazuyuki Shizawa, Crystal plasticity FE simulation for kink band formation in Mg-based LPSO phase using dislocation-based higher-order stress model, Mechanical Engineering Journal, Vol. 7, Issue 4 (2020), mej.19-00612.
(5) 屋代如月, 本多俊介, 寺田稜, 内藤圭史, 剛体Fe刃によるNiおよびCuへの押し込み切断の分子動力学シミュレーション(刃とワークの表面構造の組み合わせに着目した検討), 日本機械学会論文集, Vol. 86, No.885 (2020), transjsme.20-00061.
(6) 鯨井翔, 志澤一之, Multi-phase-fieldモデルおよび転位–結晶塑性モデルに基づくLPSO型Mg二相合金に対する動的再結晶シミュレーション, 日本機械学会論文集, Vol. 86, No. 882 (2020), transjsme.19-00341.
(7) 小林舜典, 垂水竜一, Weitzenböck多様体によるらせん転位のモデル化と数値解析, 日本機械学会論文集, Vol. 87, No. 894, (2021), transjsme.20-00409.
(8) 竹本真一郎, 吉川暢宏, メゾスケールズーミング解析によるCFRP製圧力容器の強度評価, 日本機械学会論文集, Vol. 86, No. 883 (2020), transjsme.19-00338.
(9) Keita Goto, Takuya Tomioka, Masahiro Arai, Damage-property analysis of carbon fiber-reinforced plastic based on homogenization theory, Mechanical Engineering Journal, Vol. 7, Issue 4 (2020), mej.19-00623.
(10) 菊池正太郎, 三好宏明, 松原成志朗, 奥村大, 膨潤エラストマーに対するGent-Gent超弾性モデルの有限要素実装, 日本機械学会論文集, Vol. 86, No. 890 (2020), transjsme.20-00233.
(11) 中土裕樹, 梶原ゆり, 二段階反応ピークを有する熱硬化性樹脂の硬化反応モデリング, 日本機械学会論文集, Vol. 86, No. 890 (2020), transjsme.20-00196.
3.6 計算バイオメカニクス
計算バイオメカニクスとは,生命現象を力学法則に基づいて数理モデル化し,コンピュータシミュレーションによって生体の機能や病気のメカニズムを解明しようとする研究分野である.近年の計算力学講演会では,計算バイオメカニクスに関するオーガナイズドセッションが継続的に開催され最新の研究について議論が行われてきた.コロナ禍のため,2020年度の計算力学講演会は中止になってしまったが,コロナに負けじと,若い研究者の方々が国際的な雑誌に多くの論文を発表している.本稿では,これらの論文を中心に紹介したい.
我々の骨は,破骨細胞による骨吸収と骨芽細胞による骨形成を繰り返すことで新陳代謝しており,これを骨のリモデリングと呼ぶ.骨吸収と骨形成のバランスの乱れは骨粗しょう症などの疾患の原因となるが,関連するシグナル分子のネットワーク経路が複雑であるため骨の健康状態を予測することは困難である.Kameoら(1)は,シグナル分子の反応拡散方程式,破骨細胞(骨芽細胞)への分化誘導の確率関数,有限要素法による骨の固体力学解析を連立することで,骨のリモデリングを予測するシミュレーション手法を構築した(図3-6-1左).シグナル分子(Sema3A)の発現量を増加あるいは減少させた数値実験では,動物実験で実際に観察された骨の構造と定性的に一致する計算結果が得られている(それぞれ図右のin vivoとin silico).また,薬効を予測する数値実験の方法も提案されている.定量的な薬効評価のためには多数のパラメータの同定方法など課題があるが,実用化に向けて研究が進められている心臓シミュレータ(2)のように創薬研究や臨床研究への発展が期待される.
脳血管の構造的な特徴は,複雑に分岐,吻合,合流する階層性ネットワーク構造である.脳循環には,血圧が低下あるいは上昇しても血流を一定に保とうとする自動調節機能があるが,血管のネットワーク構造が全脳循環の制御にどのように貢献しているのか十分明らかでない.Iiら(3)は,MRIから再構築した脳の実形状モデル,造影CTから抽出した動脈と静脈の実形状モデル,血管生成の数理モデルを組み合わせることで,全脳規模の血管構造を再現する手法を開発した(図3-6-2).実際のヒトの脳表層で観察される血管構造の特徴をよく再現できており,また,この脳血管モデルのフラクタル構造がラットの脳動脈のフラクタル構造と良く一致することも示された.脳のしわを仮想的に取り除く数値実験では,脳のしわが血管経路の長さに影響することも示唆されている.現在は,この脳血管モデルに対する数値流体力学解析が進められており,世界最大規模の全脳循環シミュレーションが実施されようとしている.
脳動脈瘤の破裂を予防する方法の一つにコイル塞栓術がある.これは,脳動脈瘤の中にコイルを充填することで瘤内の血流を停滞させ,血栓の形成によって塞栓する手法である.開頭手術の必要がない低侵襲かつ効果的な手法であるが,約2割の患者で塞栓が十分でなく血流の再開通が生じてしまう.血流の再開通には,瘤の大きさや形状,発生箇所,瘤内のコイルの分布や充填率などが関係していると考えられている.Otaniら(4)は,コイル塞栓術中のコイルの挙動を予測する計算モデルを開発した.共回転梁要素を用いてコイルの圧縮(引張),曲げ,ねじりから生じる応力を計算し,コイルと壁の間,またはコイル間に生じる接触力と摩擦力の方程式を連立している.コイル塞栓術だけでなく,同じく血管内治療の方法であるステント留置術の解析に対しても有効であることが示されている(5).
生体組織は多数の細胞の集まりであり,細胞活動に応じて異なる形態が形成される.細胞活動の代表的なものは細胞の増殖であり,細胞増殖によって生体組織は成長する.アクトミオシンの活性によって生じる細胞の収縮も形態形成に関与する細胞活動である.Takedaら(6)は,細胞増殖と細胞収縮の程度や順序に応じてシート状組織が異なる形態に至るメカニズムを明らかにした.組織の成長と収縮を考慮した連続体力学モデルを用いて,形態形成過程のエネルギー地形を可視化した.細胞の成長量が小さい場合にはエネルギー地形は連続であり,組織の収縮によらず一つの安定な状態(形態)に至る.一方,組織の成長量が大きくなるとエネルギー地形が不連続になり,収縮の履歴によって異なる安定状態(図3-6-3の「上に凸」あるいは「下に凸」の形態)に至るという.また,成長が進むと二つの安定状態のエネルギー障壁が大きくなるため,形態形成が擾乱の影響を受けにくくなると説明している.
生物の構造や機能をヒントにして新しい技術を作り出す研究分野をバイオミメティクスという.Nakataら(7)は,蚊の触角に着想を得た障害物センサを提案している.ロボットが障害物を検出するためのセンサとして,超音波センサや光学式センサがよく用いられる.これに対して,蚊は自身の羽ばたきによって生じる流れを感知して,壁や床を検出している可能性があるという.蚊の頭部の触角の付け根には,ジョンストン器官と呼ばれる感覚器官がある.Nakataらは数値流体力学解析を用いて,飛んでいる蚊が壁や床に近づくと頭部付近の圧力が上昇することを示した.さらに,この原理を応用した圧力センサをクアッドコプターに実装し,障害物検出システムとして有効であることを実証している.
最後に,データ科学をバイオメカニクスに応用しようとする研究を紹介する.患者個別血流シミュレーションを臨床応用するための工学的な課題は,解析にかかる時間の短縮である.Anzaiら (8)は,深層学習を用いることで,約200万格子の定常血流シミュレーションの結果を1秒以内で予測することができたと報告している.この研究では,数値流体力学解析によって得られた大動脈の流速場と圧力場をポイントクラウドとして学習させている.患者個別の血流シミュレーションは,医用画像からの血管形状の抽出,計算格子の生成,数値流体力学解析の3つの過程からなり,今回の手法では少なくとも血管形状の抽出が必要である.CTやMRIなどの医用画像DICOMデータから直接,血流を予測できるようになることが臨床研究に向けての鍵になると考える.
〔今井 陽介 神戸大学〕
参考文献
(1) Kameo, Y., Miya, Y., Hayashi, M., Nakashima, T., and Adachi, T., In silico experiments of bone remodeling explore metabolic diseases and their drug treatment, Science Advances, Vol. 6 (2020), eaax0938, DOI: 10.1126/sciadv.aax0938.
(2) Okada, J., Fujiu, K., Yoneda, K., Iwamura, T., Washio, T., Komuro, I., Hisada, T., and Sugiura, S., Ionic mechanisms of ST segment elevation in electrocardiogram during acute myocardial infarction, Journal of Physiological Sciences, Vol. 70 (2020), 36, DOI: 10.1186/s12576-020-00760-3.
(3) Ii, S., Kitade, H., Ishida, S., Imai, Y., Watanabe, Y., and Wada, S., Multiscale modeling of human cerebrovasculature: A hybrid approach using image-based geometry and a mathematical algorithm, PLoS Computational Biology, Vol. 16 (2020), e1007943, DOI: 10.1371/journal.pcbi.1007943.
(4) Otani, T., Wada, S., and Tanaka, M., Modeling of endovascular coiling for cerebral aneurysms: effects of friction on coil mechanical behaviors, International Journal of Mechanical Science, Vol. 166 (2020), 105206, DOI: 10.1016/j.ijmecsci.2019.105206.
(5) Shiozaki, S., Otani, T., Fujimura, S., Takao, H., and Wada, S., Computational modeling of braided-stent deployment for interpreting the mechanism of stent flattening, International Journal for Numerical Methods in Biomedical Engineering, 1-14 (2020), DOI: 10.1002/cnm.3335.
(6) Takeda, H., Kameo, Y., Inoue, Y., and Adachi, T., An energy landscape approach to understanding variety and robustness in tissue morphogenesis, Biomechanics and Modeling in Mechanobiology, Vol. 19 (2020), pp. 471-479, DOI: 10.1007/s10237-019-01222-5.
(7) Nakata, T., Phillips, N., Simões, P., Russell, I. J., Cheney, J. A., Walker, S. M., and Bomphery, R. J., Aerodynamic imaging by mosquitoes inspires a surface detector for autonomous flying vehicles, Science, Vol. 368 (2020), pp. 634-637, DOI: 10.1126/science.aaz9634.
(8) Li, G., Wang, H., Zhang, M., Tupin, S., Qiao, A., Liu, Y., Ohta, M., and Anzai, H., Prediction of 3D cardiovascular hemodynamics before and after coronary artery bypass surgery via deep learning, Communications Biology, Vol. 4 (2020), 99, DOI: 10.1038/s42003-020-01638-1.
3.7 逆問題・データ同化・最適化
2020年度の逆問題・データ同化・最適化の研究分野の動向について紹介する.2020年度は,新型コロナウイルスに関連する社会状況の影響を受け,計算力学講演会が中止となったため,日本機械学会年次大会における講演発表を参照する.年次大会における関連オーガナイズドセッションとして,「解析・設計の高度化・最適化」が企画され,16件の発表があった.発表内容としては,トポロジー最適化に関する発表が4件,形状最適化に関する研究が7件と半数以上が形状最適化・トポロジー最適化に関する発表であった.この中で応用研究としては,自動車用吸収部材,音響メタサーフェス,材料構造設計問題,シェル構造物など多岐に渡り,最適化分野の展開領域がさらに広がっていた.この他にも年次大会全体を通して,データ同化に関する発表が2件,トポロジー最適化に関する発表が1件,形状最適化に関する発表が2件あった.また,関連する先端技術フォーラムとしては,「バーチャルエンジニアリングにおける形状設計・計算・加工技術の現状と未来」が企画された.この中での関連講演は,新しいトポロジー最適化手法に関する発表が1件,CFRPにおけるプリントパス及び形状設計に関する発表が1件,積層造形による製造を前提としたトポロジー最適化に関する発表が2件あった.2020年度は,研究活動の形態や社会が大きく変化したことも影響し,産業界の方が著者あるいは共著者となっている発表が少なかったものの,今後も産業界からの注目が高い研究領域になると考えられる.
次に,2020年度の日本機械学会論文集における関連論文発表について調査を行った.その結果,焼き入れプロセスを対象とした熱伝導問題の感度解析法(1),マルチスケール解析を用いた吸音材料の最適設計(2),せん断型パネルダンパーの最適設計(3),シェル構造物の振動特性最適化を目的とした形状最適化(4),射出成形生産プロセスを対象とした最適設計(5),再帰ニューラルネットワークを用いた車両特性設計に対する代理モデリング法(6),帰納的アプローチによる油圧式変速機の最適設計(7),定義域絞り込みPSOと勾配法を用いた最適設計及び試験法の提案(8),配管系の動的最適設計(9)などの発表論文があった.応用展開先として,自動車,吸音材,油圧式変換器,射出成形プロセスなどがあり,機械工学全体に普及しつつあることが確認できる.2020年度に発行された日本機械学会論文集においては,逆問題及びデータ同化の論文は少なかった.年次大会等での講演発表だけではなく,今後は日本機械学会論文集での論文発表も期待したい.
次に,逆問題,データ同化,最適化の国際動向について調査を行った結果を示す.計算力学分野の代表的な国際学術雑誌である,Journal of Computational Physics (JCP) 及び Computer Methods in Applied Mechanics and Engineering (CMAME) において,2015年から2020年に出版された文献を対象として,キーワード:Inverse Problems (IP), Data Assimilation (DA), Optimal Design or Optimum Design (OD), Topology Optimization (TO),Shape Optimization (SO)で絞り込み検索を行った.キーワード毎に各年毎の文献数を整理した結果を表3-7-1に示す.
表3-7-1 JCP及びCMAMAEで発表された逆問題,データ同化,最適化関連の論文数(JCPの論文数+CMAMEの論文数)
| IP | DA | OD | TO | SO | |
| 2020年 | 151 (87+64) | 27 (14+13) | 68 (8+60) | 124 (9+115) | 136 (22+114) |
| 2019年 | 123 (69+54) | 40 (27+13) | 55 (9+46) | 111 (7+104) | 139 (28+111) |
| 2018年 | 76 (43+33) | 18 (13+5) | 49 (10+39) | 82 (10+72) | 95 (29+66) |
| 2017年 | 108 (65+43) | 23 (10+13) | 53 (12+41) | 65 (7+58) | 96 (26+70) |
| 2016年 | 66 (46+20) | 17 (14+3) | 27 (9+18) | 40 (7+33) | 69 (18+51) |
| 2015年 | 73 (48+25) | 23 (17+6) | 35 (9+26) | 53 (5+48) | 81 (16+65) |
全体として,論文数は増加傾向にあり,逆問題,データ同化,最適化の分野の注目度がより高まっていることがわかる.データ同化に関しては,論文数はほぼ横ばいであるが,逆問題やトポロジー最適化に関しては,5年間で倍増していた.トポロジー最適化に関しては,商用ソフトウエアが急拡大していることと,積層造形技術との相性が良く,積層造形技術の注目度が高まってきていることが増加の要因として考えられる.データ同化に関しても,商用ソフトウエア等の普及等により,産業界での利用がより活発になれば,今後,飛躍的に注目度が増してくると考えられる.
最適設計の分野について,2020年の国内外の動向を総説すると,特定の研究グループからの論文発表が中心から,多様な研究グループからの発表が目立つようになってきている.商用の最適化ツールの普及と産業製品への展開を念頭においた研究発表が増加傾向にあることが,多くの研究グループから注目されている要因であると考えられる.主に国際雑誌における論文数の急激な増加が目立つが,国内においても,同様の傾向が続くと考えられる.2021年度には,最適設計に関する国際会議 World Congress of Structural and Multidisciplinary Optimization が開催されるため,最新の研究動向に注目したい.また,トポロジー最適化に関しては,TOP Webinarと呼ばれるウェビナーシリーズ(10)が2020年に開始された.国際会議が相次いで中止になった中で,最新の研究動向を共有し,さらには,関連する研究者と議論できる貴重な機会となっている.なお,このウェビナーは,無料で参加登録が可能であり,誰でも参加が可能となっている.視聴のみであれば,参加登録をしなくても視聴が可能である.
一方,逆問題については,国際雑誌における注目度の高まりと比較して,国内での発表件数や日本機械学会論文集での発表数が比較的少なかった.逆問題の応用範囲は機械工学に留まらず,より広い領域に展開されていることが要因の一つであるが,機械工学においても注目され続ける分野であると考えられる.
〔山田 崇恭 東京大学〕
参考文献
(1) 古川達也, 高野直樹, 杉本剛, 木島秀弥, 田村茂之, 鋼材成分のばらつきを考慮した焼入れプロセスの相変態-熱伝導連成解析と温度に対する感度解析, 日本機械学会論文集, Vol. 86, No. 897 (2020), DOI: 10.1299/transjsme.20-00096.
(2) 山本崇史, 桂大詞, 久保田寛, 均質化法による吸音材微視構造の寸法最適化, 日本機械学会論文集, Vol. 86, No. 889 (2020), DOI: 10.1299/transjsme.20-00073.
(3) 繰り返し荷重を受けるせん断型パネルダンパーの最適設計, 日本機械学会論文集, Vol. 86, No. 891 (2020), DOI: 10.1299/transjsme.20-00046.
(4) 史金星, 下田昌利, 酒井忍, CFRP板・シェル構造の固有振動問題に対するフリーフォルム最適設計, 日本機械学会論文集, Vol. 86, No. 891 (2020), DOI: 10.1299/transjsme.20-00128.
(5) 北山哲士, 橋本咲良, 高野昌宏, 山崎祐亮, 久保義和, 合葉修司, プラスチック射出成形における可変射出速度と可変保圧力を用いたウェルドラインとサイクルタイムの二目的最適設計, 日本機械学会論文集, Vol. 86, No. 891 (2020), DOI: 10.1299/transjsme.20-00161.
(6) 牧野晃平, 三輪誠, 新谷浩平, 阿部充治, 佐々木裕, 再帰ニューラルネットを用いた車両運動性の代理モデリング, 日本機械学会論文集, Vol. 86, No. 891 (2020), DOI: 10.1299/transjsme.20-00177.
(7) 中川修一, 池上聡一郎, 深田和範, 大内田剛史, 帰納的アプローチによる油圧式変速機の最適設計プロセス, 日本機械学会論文集, Vol. 86, No. 890 (2020), DOI: 10.1299/transjsme.20-00268.
(8) 本堂貴敏, 空気圧式可変長高さ調整棒を用いた高さ調整弁の過渡特性同定法(定義域絞り込みPSOと勾配法による最適化法と試験法の提案), 日本機械学会論文集, Vol. 86, No. 890 (2020), DOI: 10.1299/transjsme.20-00232.
(9) 山崎一生, 平元和彦, 慣性質量要素を有する振動制御デバイスを適用した配管系の動的最適設計, 日本機械学会論文集, Vol. 86, No. 891(2020), DOI: 10.1299/transjsme.20-00059.
(10) https://www.youtube.com/channel/UCfknafkFQBuTOtHJH8I4qLQ
3.8 機械学習と計算力学の融合
2016年以降,機械学習に関する研究開発が急速に進み,広がりを見せている.機械学習とは,AIだけではなく,データドリブンな方法であり,単なる予測器を生成するだけではなく,物理現象も再現する代替モデル構築まで可能な手法として期待されている.代替モデルはSurrogate Modelとも言われておりいくつかの手法により構築が可能である.
・深層学習(1)
・ガウス過程(1)
・ベイズ学習(1)
・スパースモデリング(2)
などこれら以外にも古典的方法も含めれば構築可能な手法は多数あり,日々アルゴリズムの改良が行われている.機械学習はここ数年で急速に適用事例が増加した分野である.機械学習に関する手法の多くの共通の目的は,時間のかかる順問題や逆問題のプロセスを高速化することである.また,高速化自体が目的でない場合は,同定が困難なシステムの代替モデル構築自体が目的である.深層学習とその他の方法の大きな違いは必要とするデータ量の違いである.深層学習では多くのデータにより汎化能力を高めるが,ガウス過程などは比較して少ないデータで予測器の生成ができるが精度に問題が残る.個々の研究では,
・予測したい問題の複雑さ(ほぼ線形であれば重回帰分析などでもよい),
・データ量がどの程度か(予測したい問題の複雑さに比べて),
・事前に仮定できるモデルはあるのか,
などにより選択する手法が異なる.したがって,どの手法が優れているかという観点より,対象としている問題にどの手法が適しているのかどうかが重要である.一方で,少ない(一般な工学問題においてデータ計測や生成はコストが高い)教師データを増やすことは,より良い予測には必要条件である.一般的なデータ拡張は画像の回転やノイズ付与などであるがその他にも性質を変えずにデータを拡張する方法の適用が汎化性能向上のため重要である(3).2020年はコロナ禍で多くの学会が中止またはオンラインとなり情報収集という観点では不十分であったと感じている.本稿では,2019年12月に開催されたAPCOM2019(4)から2020年に開催された国際会議等も含めて機械学習の最新動向について記す.
第33回計算力学講演会(2020年9月開催予定であったが中止)においても機械学習に関するセッションを企画したが中止のため論文の募集とまでは至らなかった.日本計算工学講演会においても講演自体は中止となったが予稿集は発刊(5)した.当初18件の申込みがあったが,中止のため取り下げが生じ,13件が掲載されることになった.ここ数年,国内学会である計算力学講演会などや,APCOMなどに代表されるIACM傘下の国際学会においてオーガナイズドセッションやミニシンポジウムで20件前後の申込みがあり,研究活動は引き続き活発に行われている.機械工学年鑑2018では,「画像解析による応用はその事例は多数見受けられるが,一方で物理現象,工学設計における応用方法が全く示されていないまたは画像的な取扱でデータ学習させる傾向が強くある」(6)と指摘させていただいた.現状では工学問題に適した応用,利用方法が活発に検討されており,さらなる応用・発展の可能性を感じられるまでになった.
機械学習を実装するための開発環境はほぼデファクトスタンダード化がすすんでおり,LinuxシステムにNVIDIAの開発環境をGPU機にインストールしてあり,電源をいれればすぐに機械学習が始められる.数十年前のワークステーションの初期設定を丸一日かけて行ったことに比べると感慨深い.これらは,Docker(7)に代表される仮想コンテナ技術で実現されており,環境構築が容易に行えるようになったのも技術的な進歩として恩恵を受けている.
USACMでは,2021年9月に,データサイエンスに特化した講演会である,第1回Mechanistic Machine Learning and Digital Twins for Computational Science, Engineering & Technology(MMLDT-CSET2021)(8)が米国サンディエゴで開催される.筆者もミニシンポジウムを企画した.8つの応用領域を表すトラックが設定されており,そのトラックにミニシンポジウムが合計44件企画された.Computational Mechanicsではなく,あえてComputational ScienceやEngineeringという言葉を用いて間口を広げたためより幅広いミニシンポジウムの企画が集まったと思われる.ここで重要な3つのキーワードが散見される.
・Digital Twins
・Data-Driven
・Reduced-Order Modeling
どのキーワードも以前からあるものだが,機械学習や統計数理などの分野と結びつき,より有効な手法開発,応用方法の研究が進められていると理解できる.
深層学習に関して有益な論文はいくつかあるが,筆者が注目しているいくつかの論文が示唆していることがある.
・深層にすると大域的ミニマムと局所ミニマムがほぼ一致することが予測されている(9)
・深層にすると表現能力が格段に向上する(10)
・汎化性能向上のための手法はすべてが有効なわけではない(画像で有効でも回帰問題では適用しないほうがよいこともある)(11)
深層にしたほうが良いのだが,深層学習を達成するためのデータがそもそも多くないという問題が常に付きまとう.こういった深層学習が持つであろう性質を適切に利用した応用方法の提案が望まれる.今後,ますます計算力学分野における機械学習手法が適用されると期待するが,学習対象を可能な限り正しく理解し,教師データの特性や統計的性質を理解し,さらに,利用する機械アルゴリズム学習アルゴリズムの特徴をうまく引き出すことが高度な応用に不可欠である.これらを通じて,機械学習と計算力学の融合が実現する.この融合された成果は,基盤技術としてDigital Twinsを実装するシステムに組み込まれる.Digital Twinsの実現が,機械学習と計算力学の融合の実例として,大きな節目になると考える.
〔和田 義孝 近畿大学〕
参考文献
(1) C.M.ビショップ, パターン認識と機械学習 上/下 ベイズ推論による統計的予測, 2012,丸善
(2) 藤本 晃司, 田中 利幸, スパースモデリングと医用MRI(<特集>スパースモデリング: 情報処理の新しい流れ), 応用数理, 25巻1号, pp.10-14, 2015
(3) 和田義孝, 深層学習によるサロゲートモデル構築, プラスチック成形加工学会誌, Vol.32, No.3, pp.83-86, 2020
(4) APCOM2019 site, http://www.apcom2019.org/(参照日 2021年4月1日)
(5) 第25回計算工学講演会予稿集, https://confit.atlas.jp/guide/event/jsces25/top(参照日 2021年4月1日)
(6) 機械工学年鑑2018, https://www.jsme.or.jp/kikainenkan2018/(参照日 2021年4月1日)
(7) Docker site, https://www.docker.com/why-docker (参照日 2021年4月1日)
(8) MMLDT-CSET 2021 site, https://sites.google.com/eng.ucsd.edu/iacm-mldt-cse(参照日 2021年4月1日)
(9) A. Choromanska, et al., The loss surfaces of multilayer networks, arXiv:1412.0233 (cs.LG), 13 pages, 2015.
(10) G. Montúfar, et al., On the Number of Linear Regions of Deep Neural Networks, Twenty-eighth Conference on Neural Information Processing Systems, 9 pages, 2014.
(11) C. Zhang, et al., Understanding deep learning requires rethinking generalization, 5th International Conference on Learning Representations, 15 pages, 2017.
3.9 産業界での計算力学
産業界における計算力学は,基礎的な現象の解明のための小規模なモデル,流体や構造など複数の現象が連成したマルチフィジックス,さらに,大規模なモデルを用いたシミュレーションと,基本的なモデルから実用的なモデルへの応用と多岐にわたって取組が行われている.
2020年はCOVID-19の感染拡大の影響で中止となった機械学会計算力学部門講演会にかわり,当該分野の研究の進捗やCAEアプリケーションソフトウェアの発展などの最新情報の発信を目的に「CMD2020計力スクウェア研究報告集」(1)が発行された.産業界からは20編の研究事例が収録されている.各種シミュレーション技術に関するものに加えて,データ連携技術やCAE教育などの事例も紹介されている.基本的なモデルとして,金属材料の延性破壊現象(2)やマイクロ波プラズマ放電(3)などの基本現象メカニズムの解明に関する研究,塗布工程の流動シミュレーション(4)などの研究が報告されている.マルチフィジックスとして,積層構造の流体構造連成解析や音響構造連成解析(5)の研究が報告されている.また,プラットフォーム活用のデータ連携技術(6)やポスト処理とレポート作成の自動化(7),商用コードによる大学での教育(8)などが紹介されている.
産業界ではソフトウェアの品質保証の観点から汎用コードが多く用いられている(9).その一方で,汎用コードでは対応できない複雑な現象に対しては,大学や公的な研究機関との産官学連携により,モデルの開発やコードの開発などの研究が行われている.狭窄血管動解析の流体構造連成アルゴリズム開発(10)やポンプ内のオイル飛散挙動の解析(11),接触問題のアルゴリズム開発(12)や破壊モデルの構築(13)などの研究が報告されている.また,2020年はCOVID-19の感染拡大に関して,本格的な共用開始を前にスーパーコンピュータ「富岳」(14)を用いて,感染リスク評価や対策提案を目的に,室内環境や列車内などの飛沫やエアロゾルの飛散の様子のシミュレーションが行われた(15).
AIと計算力学の融合が注目されている.例えば,ベイズ最適化による弾塑性解析パラメータの同定(16)や固有直交分解による固体酸化物形燃料電池の電気化学ポテンシャル解析(17)などの研究が報告されている.CAE懇話会では「ディープラーニングとCAE(第4回)~機械学習・統計数理とCAEの融合による新しい世界~」(18)というテーマで産業界からも事例が紹介され,活発な議論が行われている.産業界ではこれまで,計算力学は主に機器の開発や設計の時に多く用いられ,計算機能力とともに発展してきた.これからは開発や設計の時だけでなく,オペレーションやメンテナンスへの応用が重要である.特に,オペレーションではリアルタイムなシミュレーションが求められている.実機から得られたデータだけでなく,大規模解析などから得られたデータを教師データに用いたReduced Order Model(ROM)の構築など,AIと計算力学の融合が期待されている.
2020年9月に開催された機械学会年次大会(19)において計算力学部門では他部門と共同企画で「Society5.0を支える計算情報科学基盤の深化と進展」と題した先端技術フォーラムが開催された.Society5.0(20)が掲げている「サイバー空間(仮想空間)とフィジカル空間(現実空間)を高度に融合させたシステムにより,経済発展と社会的課題の解決を両立する,人間中心の社会(Society)」を実現するための科学的アプローチとして,人・社会とシステム・サービスの不確かさを含めたモデリングに関してさらなる深化について議論された.さらに,対象領域を工業製品の設計・生産・サービスから,医療・社会インフラ・海洋分野を含めた広範囲の社会課題への取組の進展の共有がはかられ,製造業におけるスマート・サービス実現のためにサイバーフィジカルシステム(Cyber Physical System,CPS)上に製品・生産・調達・販売・サービスのデジタルツインの開発・構築などの取組が紹介された(21).このなかでも,世界的なCOVID-19感染拡大の状況化で,様々な領域で従来の概念を大きく変革する必要性が認識された.地球規模で発生する災害や感染症拡大などをCPS上で精度よく予測し,安心・安全,持続可能性,回復力を提供する新たな社会システムとしてSociety5.1が定義され,計算情報科学基盤に予測科学の追加が低減されている.
国際的な脱炭素化の流れのなか,2020年10月に2050年カーボンニュートラル,脱炭素社会の実現を目指すことが宣言され(22),2050年カーボンニュートラルに伴うグリーン成長戦略(23)が報告された.産業界に対しては,実現に向けた研究開発と社会実装が期待されている.これに向けて産官学連携し,本格運用が開始された「富岳」を代表とする高性能な計算機を活用するなどして要求に応えていくとともに,今後ますます必要とされる計算力学に関する人材の育成が期待されている.
〔神保 智彦 (株)東芝〕
参考文献
(1)CMD2020計力スクウェア研究報告集,日本機械学会
https://www.jsme.or.jp/cmd/japanese/events/2020/cmd2020_report.pdf(参照日2021年3月15日)
(2)鈴木翔,金伝栄,顧文煒,張衛紅,理想化陽解法による切欠付丸棒引張試験の損傷力学解析の試み,CMD2020計力スクウェア研究報告集,(2020),Report No.1-01.
(3)佟立柱,有限要素法を用いたマイクロ波プラズマシミュレーション,CMD2020計力スクウェア研究報告集,(2020),Report No.1-14.
(4)篠崎明,塗布工程の流動シミュレーション,CMD2020計力スクウェア研究報告集(2020),Report No.1-19.
(5)米大海,橋口真宜,有限要素法を用いた積層構造の連成解析,CMD2020計力スクウェア研究報告集,(2020),Report No.1-04.
(6)眞崎浩一,小坂部和也,大谷英之,プラットフォーム活用のためのデータ連携技術,CMD2020計力スクウェア研究報告集,(2020),Report No.1-11.
(7)宮本裕平,眞崎浩一,CAE解析におけるポスト処理とレポート作成の自動化,CMD2020計力スクウェア研究報告集,(2020),Report No.1-12.
(8)金哲晃,杉本康弘.佐々木大輔,商用ソフトウェアを使用した大学でのCFD教育,CMD2020計力スクウェア研究報告集,(2020),Report No.1-18.
(9)左海将之,塩谷篤,青木泰高,数値解析を活用した気液二相流分配評価技術の開発,三菱重工技報,Vol.57,No.1,(2020).
(10)和久智裕,浜砂望,渡邉浩志,立石源治,波多野明日可,狭窄血管動解析のための流体構造連成co-simulationアルゴリズムの開発,CMD2020計力スクウェア研究報告集,(2020),Report No.1-17.
(11)油橋信宏,越塚誠一,往復動ポンプにおけるクランクケース内のオイル飛散挙動の予測(MPS法を用いた自由表面流れの解析),日本機械学会論文集,vol86,No.881(2020),DOI:10.1299/transjsme.19-00343.
(12)月野誠,山田貴博,反復法のための安定化手法を用いたNitscheの方法による有限被覆法3次元接触解析,日本計算工学論文集(2020),Paper No.20200021.
(13)韓霽珂,西紳之介,高田賢治,村松眞由,大宮正毅,小川賢介,生出佳,小林卓哉,村田真伸,森口周二,寺田賢二郎,可変正則化パラメータを用いたphase-field延性破壊モデル,日本計算工学論文集(2020),Paper No.20200005.
(14)スーパーコンピュータ「富岳」について,理研
https://www.r-ccs.riken.jp/jp/fugaku(参照日2021年3月15日)
(15)室内環境におけるウイルス飛沫感染の予測とその対策,理研
https://www.r-ccs.riken.jp/jp/fugaku/corona/projects/tsubokura.html(参照日2021年3月15日)
(16)泉優行,金伝栄,顧文煒,鈴木翔,機械学習アルゴリズムを用いた弾塑性解析パラメータの同定,CMD2020計力スクウェア研究報告集,(2020),Report No.1-05.
(17)佐藤維美,村松眞由,外里健太,森口周二,川田達也,寺田賢二郎,固有値直交分解を用いた固体酸化物形燃料電池の電気化学ポテンシャル解析,CMD2020計力スクウェア研究報告集,(2020),Report No.1-10.
(18)第74回関西CAE懇話会,CAE懇話会
http://www.cae21.org/kansai_cae/konwakai/kansai_74/kansai74_annai.shtml(参照日2021年3月15日)
(19)日本機械学会2020年度年次大会,日本機械学会
https://jsmempd.com/conference/jsme_annual/2020/(参照日2021年3月15日)
(20)Society5.0,内閣府
https://www8.cao.go.jp/cstp/society5_0/(参照日2021年3月15日)
(21)平野徹,Society5.0を支える人・社会とシステム・サービスの不確かさを含めたモデリング・シミュレーション,CMD Newsletter,No.64,(2020).
(22)2050年カーボンニュートラルの実現に向けて,環境省
http://www.env.go.jp/earth/2050carbon_neutral.html(参照日2021年3月15日)
(23)成長戦略会議(第6回)配布資料,内閣官房
https://www.cas.go.jp/jp/seisaku/seicho/seichosenryakukaigi/dai6/index.html(参照日2020年3月15日)
3.10 防災関連
2011年3月の東日本大震災の復興予算も累計20兆円を超えた.その後も我が国では,2015年9月関東・東北豪雨災害,2017年7月九州北部豪雨,2018年7月の西日本豪雨,2020年7月豪雨(球磨川氾濫)などの気象災害が相次いでおり,そのたびに復興予算を計上し,国家予算を逼迫する原因となっている.自然災害からの人災ゼロを実現するためだけでなく,国家予算の支出を最小限に留めるためにも,被害を最小限に留める方策を適切に計画しなければならない.
こうした背景から,特に2011年の東日本大震災以降,災害の被害予測に資する数値計算技術の開発が加速し,たとえば2014年に災害の数値計算に関する国際会議(COMPSAFE:Computational Engineering and Science for Safety and Environmental Problems)(1)が仙台で開催され,2017年には中国・成都で,そして第3回目が2020年12月に神戸でオンライン開催された.新型コロナの影響を受け当初の予定より1年近く延期され,オンライン会議が余儀なくされたものの,375件の発表があり,発表者数が過去2回を上回った.国内でも,たとえば計算力学部門が開催している計算力学講演会でも,社会・環境・防災シミュレーションが毎年企画され,学際的な議論が展開されている.
災害被害予測に資する計算技術は年々高度化されており,最近の注目すべきキーワードとしては,京あるいは富岳などのスパコンを使ったHPC援用の都市まるごと解析(2),あるいは災害の本質である不確実性の定量化(3)など,データサイエンスとの融合があげられる.この中でも注目すべき研究例を紹介する.
東京大学地震研究所の市村・藤田・堀・Lalithらのグループは,京,富岳,Oakforest-PACS,Summitなど様々なアーキテクチャおよびシステムで良好な性能を示す大規模高性能並列計算によるスケーラブルな有限要素ソルバーを開発し,都市の地震時応答解析を実現してきた.最近では,高性能な並列計算のため,最新のアーキテクチャ等の計算機の特性を考慮するだけでなく,求解過程を機械学習で学習させた独自の前処理付連立一次方程式解法を提案することで,富岳全系までスケールさせている.これまでは表層地盤と地表面の構造物を対象とした都市規模解析を行ってきたが,図3-10-1に示すように,最先端のソルバーにより50㎝程度のメッシュで解析することができ,従来は難しかった2×2kmの範囲の地盤と地上・地下構造物の完全連成系都市モデル(0.5mの非構造四面体二次要素25.9億要素による110億自由度のモデル)の地震時応答を富岳2048ノードにより高速に解析した.アーキテクチャ,システム,物理シミュレーション,データ学習の適切な連携は,従来とは異なる新たなアルゴリズム開発の可能性を示している.
図3-10-1 地上・地下構造物と地盤の完全連成系都市モデル(110億自由度)
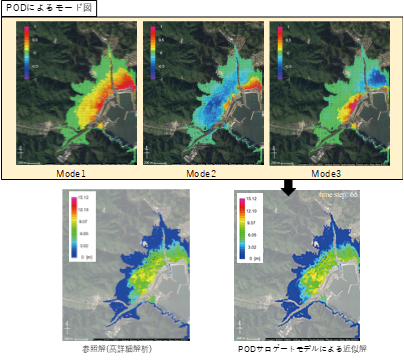
東北大学災害科学国際研究所の寺田・森口らのグループは,災害の本質である不確実性を考慮した都市規模の津波解析を可能とした.対象としては2011年の津波被害を受けた岩手県田老町をとりあげ,2次元浅水長波解析と3次元流体解析を連成させることで,遡上後の浸水深だけでなく,構造物に作用する力の評価まで実施した.さらには不確実性を考慮した多数回の計算を省力化する,あるいはリアルタイムで高詳細と同様な予測を実現するために,固有値直交分解(POD)によるサロゲートモデルを提案している(図3-10-2参照).先の地震時の研究と同様に,防災分野のシミュレーションにおいてもデータサイエンスと計算力学の融合がこれからのトレンドとなるであろう.
図3-10-2 PODサロゲートモデルによる津波浸水深の高速計算(3)
その他の重要なトピックスはマルチフィジックス解析である.信頼性の高い災害情報を提示するには,構造物・水・粒状地盤などの多種多様な材料の変形・破壊・運動・流れといった様々な現象を精緻にモデル化しなければならない.日本計算工学会・多元災害シミュレーション研究会(4)では,このような災害に関わる種々の物理現象を精度良く再現し,防災・減災に役立つ高確度情報として提示するための計算工学の枠組みを構築することを目的とし,異分野交流を通して新しい計算理論・技術の創成を図るとともに,「計算防災学」の体系化を目指した議論を行っている.
〔浅井 光輝 九州大学〕
参考文献
(1) https://compsafe2020.org/
(2) Tsuyoshi Ichimura, Kohei Fujita, Takuma Yamaguchi, Akira Naruse, Jack C. Wells, Thomas C. Schulthess, Tjerk P. Straatsma, Christopher J. Zimmer, Maxime Martinasso, Kengo Nakajima, Muneo Hori, Lalith Maddegedara, A fast scalable implicit solver for nonlinear time-evolution earthquake city problem on low-ordered unstructured finite elements with artificial intelligence and transprecision computing, SC ’18 Proceedings of the International Conference for High Performance Computing, Networking, Storage, and Analysis, Article No. 49 (2018).
(3) Tozato, K., Takase, S., Moriguchi, S., Terada, K., Otake, Y., Fukutani, Y., Nojima, K., Sakuraba, M., and Yokosu, H.: Real-time Tsunami Force Prediction by Mode Decomposition-Based Surrogate Modeling, Nat. Hazards Earth Syst. Sci. Discuss. [preprint], https://doi.org/10.5194/nhess-2021-77, in review (2021).
(4) https://www.jsces.org/activity/research/saigai/