関連部門ホームページ・関連部門イベント

章内目次

5.1　まえがき
5.2　材料工学におけるAI，IoTの活用の現状
　5.2.1　材料工学へのAI技術の融合／5.2.2　大型プロジェクト
5.3　原子間ポテンシャル開発における機械学習・深層学習の活用
5.4　ディープラーニングによる外観検査
　5.4.1　ディープラーニングによる外観検査の問題点／5.4.2　Autoencoderによる異常検知／5.4.3　GANsによる異常検知／5.4.4　適用事例
5.5　ペリダイナミクス
　5.5.1　はじめに／5.5.2　ペリダイナミクスの3つの定式／5.5.3　課題と応用例

5.1　まえがき

　2018年12月，羽生善治竜王が防衛に失敗し27年ぶりに無冠となった．将棋界では若手棋士の台頭が目覚ましいが，人工知能，すなわちAI（Artificial Intelligence）を取り入れた戦法研究が盛んになされていると聞く．塾での学習にもAIが取り入れられるなど，現在は第三次AIブーム（2006年～）の真っ只中にあるようである．筆者は第二次AIブーム（1980年～1987年）頃にコンピュータの世界に足を入れたが，クロックスピード5MHz，メモリ128KBのCPU性能，そして20MBのハードディスクが10万円という，当時のコンピュータや周辺機器の性能ではAIは夢物語に過ぎずにブームはすぐ終焉した．半導体・ネットワーク・デジタル技術の爆発的な発展によって，現在では指先に乗るマイクロSDカードに256GBのデータを格納でき，かつ数千円程度で入手できる．身近な家電製品にも少し前のパソコンより高性能なコンピュータが用いられ，スマートスピーカーによって声で操作できる時代になった．このように膨大なデータを収集・保有・処理する能力を持ち，かつネットワークで相互にデータを共有する時代において，AIはその存在感を増している．

　AI研究の動向について，計算力学部門では昨年度の機械工学年鑑で取り上げていたが，材料力学の分野ではまだ端緒についたばかりと思われる．膨大な胃カメラ画像をAIに学習させて初期がんの早期発見に結び付ける医療分野での動きのように，フラクトグラフィや寿命診断にAIを活用する動きは今後出てくるものと考える．そこで今回は，AI，ビッグデータなどのインフォマティクスやシミュレーション，画像処理にスポットを当てることにして，材料工学におけるAI，IoTの活用の現状，原子間ポテンシャル開発における機械学習・深層学習の活用，画像処理のディープラーニングによる外観検査，連続体近似のFEMでは難しかった破壊現象を扱えるマルチフィジックス・マルチスケールシミュレーション手法のperidynamicsなど，筆者が興味を持っている分野の第一人者の方々にご寄稿いただいた．

〔屋代　如月　岐阜大学〕

目次に戻る

5.2　材料工学におけるAI，IoTの活用の現状

5.2.1　材料工学へのAI技術の融合

　他の分野と同様に社会基盤材料の分野でもさまざまな側面でAI，IoTが注目され，様々なプロジェクトが進められている．これらの分野は，マテリアルズインフォマティクス，プロセスインフォマティクス，計測インフォマティクスと呼ばれている．例えば，鉄鋼協会の講演大会での発表を見ると，鉄鋼の原料配送計画，生産設備の操業条件の最適化，品質管理，そして今日では研究開発の広範囲においてIoT技術，データサイエンス，機械学習に関する講演が見受けられる．研究の側面では，機械学習単独ということではなく，モデリングあるいは実験と併用して，効率的，複雑な現象の影響度解析（感度解析），逆解析などに機械学習が用いられている．

　材料工学は，プロセス―組織―特性の関係を理解する際に，組織を定量評価することが重要となるが，定量評価する事前準備として組織写真の二値化処理が必要となる．複雑なコントラストを有する材料組織写真を，汎用画像処理ソフトによる輝度値に基づいた二値化処理した場合は，必ずしも満足のいく領域抽出が行われない場合が多い．そこで最近では，画像工学の分野で用いられるようになってきている機械学習やディープラーニングを使った領域抽出アルゴリズムにより，材料組織の領域抽出が行われるようになってきている．フリーソフトImageJを使ったWeka trainable segmentation，ディープラーニングではmask R-CNN，Segenet，U-netなどの材料組織中の領域抽出への適用が報告されている．

　プロセス→組織→特性の順方向の関係把握（順解析）に加えて，逆方向の傾向把握（逆解析）に機械学習を活用することに注目が集まっている．アルゴリズムとしては，遺伝的アルゴリズム，粒子群最適化，ベイズ的最適化などが提案されている．順解析のアルゴリズムとしては，ニューラルネットワーク，カーネル法を取り入れたサポートベクター回帰，複数の決定木を使ったランダムフォレスト回帰，非線形の重回帰分析であるガウスプロセス回帰などが用いられている．

　時系列データに対しては，再帰型ニューラルネットワーク（recurrent neural network: RNN）が有用である．ひとつ前のニューラルネットワークの隠れ層情報が現在のニューラルネットワークの隠れ層に入力され，短期間情報記憶が行われる．更にその発展形として，短期・長期を記憶するlong short term memory（LSTM）というアルゴリズムも報告されており，今後疲労やクリープ減少などの時系列データへの適用が期待される．

　実画像に類似した画像を人工的に創成するアルゴリズムである敵対的生成ネットワーク（Genera tive Adversarial Networks: GAN）は，画像データ数増加の効率的手法として今後注視する必要があるであろう．

　これらの材料工学に使える機械学習法を統合した材料情報統合システムが国内でもいくつか提案されている．例えば，名古屋大学MIPHAとshinyMIPHA，物質・材料研究機構のMaDISなどが報告されている．スタンドアロン型，クラウド型など提供方法もさまざまであり，言語はPython, Visual Basic, Rなどが用いられている．

5.2.2　大型プロジェクト

　材料工学へのAIの導入を促進することを狙った大型プロジェクトとしては，内閣府のSIPプロジェクト二期，CRESTの［革新材料開発］実験と理論・計算・データ科学を融合した材料開発の革新，［情報計測］計測技術と高度情報処理の融合によるインテリジェント計測・解析手法の開発と応用，日本学術振興会の「自律型・複合型AI先端計測の新しい価値創造」研究開発専門委員会，NEDOが支援する「省エネ製品開発の加速化に向けた複合計測分析システム研究開発事業」が進められている．

〔足立　吉隆　名古屋大学〕

目次に戻る

5.3　原子間ポテンシャル開発における機械学習・深層学習の活用

　ある環境下における物質の挙動をnmあるいはÅの解像度で明らかにすることは，現象の本質的理解を目指すうえで自然な要求である．モンテカルロ法や分子動力学法などの原子モデルシミュレーションはそれゆえ長い歴史を持ち，1950年代には既に試みられていた．原子間相互作用の評価には当初は極めて単純な，原子間距離のみに依存する関数である二体間原子間ポテンシャルが用いられたが，計算機能力の向上とともにより精度の高い複雑な形の関数が用いられるようになっていく．凝集系では材料によって様々な原子間結合状態が形成されるとともに，結合状態がしばしば原子の多体効果の影響を強く受けるため，材料のシミュレーションでは複雑な関数形の原子間ポテンシャル関数構築が必要となるケースがほとんどである．原子間の相互作用は，第一原理計算のようなSchrödinger方程式を陽に取扱い電子状態を求める方法を用いれば精度良く評価することができるが，並列・超並列の高性能計算機を長時間占有できる場合を除いて，第一原理計算により材料の変形や破壊のシミュレーションを行うことは現実的でない．そのため，材料力学分野で原子系のシミュレーションが広まり始めた1990年代以降の長きにわたり，材料に対する精度のよいポテンシャル関数の構築は重要な問題であり続けている．

　一般的な原子間ポテンシャル（ここでは従来型と呼ぶ）の構築においては通常，原子構造の情報（原子間距離や角度など）を変数とする関数形が予め設定され，関数に含まれる数々のパラメータを調整することでそのポテンシャルが目的の物性値（リファレンスデータと呼ばれる）を再現できるようにするという手続きが取られる．関数形を決定する時点でパラメータの数も固定されるため関数最適化の自由度が規定されることとなり，また原子構造因子に対する依存性についても規定してしまうこととなる（例えば三体項以上の関数を含まないポテンシャルでは結合角依存性は全く表現できない）．すなわち対象とする材料の原子結合の振舞いを熟知したうえで適切な関数形を設定することが求められ，リファレンスデータの取得やパラメータ最適化を非経験的方法で行ったとしても，得られたポテンシャルは経験的なものとなるのが大きな問題であった．

　ポテンシャル関数構築をよりシステマティックな方法で行うために機械学習や深層学習の手法を導入する試みが2000年代後半より活発になされるようになってきた．これは原子間ポテンシャル関数構築が，材料学的あるいは物理化学的な問題から数理工学・データサイエンス的問題に変化するという意味で，大きなパラダイムシフトが起こりつつあるという見方もできる．本稿ではそのような取組みのうち最も注目されていると言える，Behler・Parrinelloらによる人工ニューラルネットワーク導入の取組み^{（1）（2）}を中心に，本問題の研究動向を紹介する．なお，機械学習の定義は曖昧であり，例えば遺伝的アルゴリズムのような一般的な最適値探索法もこれに含められる場合が稀にあるが，このような広義の機械学習を考えてしまうと，従来型の方法で構築された経験的ポテンシャルもパラメータ最適化を計算機が行ったという理由で「機械学習に基づく原子間ポテンシャル」となってしまうため，ここではそのようなアプローチは除外する．

　人工ニューラルネットワーク自体の歴史は長く，1940年代にMcCulloch・Pittsにより神経系のシグナル伝達を模擬するためのシンプルな数学的モデルとして人工ニューロンが提案^（3）された後，入力層と出力層を複数の人工ニューロンで接続する初期の人工ニューラルネットワークが提案された（Rosenblattのパーセプトロン^（4））．その後数々の改良が加えられ，特に1980~1990年代に急速な発展を遂げ，未知の関数を近似することができる万能型のモデルとして認識されるようになり，様々な用途に応用されるようになった^{（5）（6）}．1995年にBlankらによって最初のニューラルネットワーク原子間ポテンシャル（Neural Network Interatomic Potential: NNP）が提案され^（7），その後多くの適用例が発表されることとなる．これは，原子構造を入力情報として，その構造におけるポテンシャルエネルギーを出力する，すなわち原子構造というベクトル情報からポテンシャルエネルギーというスカラー値への写像を模擬するニューラルネットワークモデルを作成するというアイデアである．

　NNPの構築において重要となるのが，物理的な描像を持たない数学的モデルにおいて原子構造をいかにして表現するか，という点である．この点においてBehler・Parrinelloが2007年に発表した方法（High-Dimensional NNP: HDNNP^（1））は大きなブレークスルーを与えた．HDNNPでは系のポテンシャルE_sは各原子（iで表す）のポテンシャルエネルギーE_iの総和で表すものとするため，NNPの構築は，原子iの近傍にある原子群の配置を表現し（入力層），原子iのポテンシャルエネルギーを出力するニューラルネットワークを作成するという問題に帰着される．原子配置の表現としてBehlerらは，配位数に対応する$G_i^1$，放射対称（radial symmetric）関数$G_i^2$，角度対称（angular symmetric）関数$G_i^4$などを用いて表現する方法を提案した．式を以下に示す．これらを基底関数として周囲の原子配置を表現する方法は広く用いられるようになっている．Artrith・Urbanらはこの手法に基づいてNNPを構築する手続きをオープンソースのパッケージ（atomic energy network: ænet）として公開しており^（8），NNP構築に対する技術的な障壁が大幅に軽減された．従って，今後は様々な系に対するNNP構築の取組みがますます加速していくものと予想される．

　NNPと従来型の原子間ポテンシャルの決定的な違いは，NNPが原子間結合状態などの物理的な描像に立脚していない点にある．従来型では一般に，原子間ポテンシャルエネルギーが二体間相互作用（距離のみに依存）や多体効果（結合角・二面角依存などを含む）などから構成される（それが関数形として表記される，言い換えれば作成された関数形がポテンシャルエネルギー発現の物理的機序を物語っている）のに対して，NNPではこうした情報が表に現れない，すなわちポテンシャルエネルギーの発現メカニズムが完全にブラックボックス化される．そのため，作成されたNNPの適用可能範囲には特に注意する必要がある．ポテンシャル構築の際にはフィッティングのためのリファレンスデータ（教師データ）を一定数用意しておき，そのうちの一部をテストセット，それ以外をトレーニングセットとしておき，トレーニングセットのみをフィッティングに使用してテストセットを用いて妥当性検証を行うのが常套手段であるが，NNPの場合には検証された構造以外への外挿を許すことは危険である．また，教師データの再現性を良くしすぎたためにそれ以外の構造に対する精度が著しく損なわれるオーバーフィッティング問題にも注意すべきである．こうした問題への処方箋についてもBehlerらによって具体的に提案されている^（9）．

　これまで様々な系に対するNNP構築例が発表されている．分子系に対しては1990年代より多くのNNPモデルが発表されている^（9）．一方，結晶構造・凝集系に対してはそれほど多くない．BehlerらのグループによりSiの高圧相への相変態を記述可能なモデル^{（1）（10）}，Naの液相から高温・高圧下の固相への相変態を記述できるモデル^{（11）（12）}，Cのグラファイトからダイヤモンド相への相変態を再現するモデル^（13），ZuO表面・Cuクラスター系のモデル^{（14）-（17）}，水とCuの固液界面を再現するモデル^（18）が発表され，KobayashiらはAl-Mg-Si合金系へのNNPモデルを発表している^（19）．上述のようにNNP構築の技術的な障壁は下げられているため，今後多くのNNPモデル構築例が発表されることと思われる．

　その他にも，機械学習による原子間ポテンシャルと呼ばれるものとしてはBartokらによるガウシアン近似ポテンシャル（GAP）が知られている^（20）．これはガウス過程回帰で原子間相互作用を記述し，相互作用を二体間・三体間・多体間と展開してカーネルと呼ばれる構造記述子で表現するものであり，NNP同様に物理的描像に基づかないポテンシャル表現という意味で機械学習的なモデルに分類される．Si結晶への適用例が発表されており^（21），様々な結晶構造のエネルギー・欠陥エネルギー評価・破壊の解析への有効性が示されているが，その他の材料への適用はあまりなされておらず今後の展開が期待される．

　また，従来型のポテンシャル関数を用いるものの，パラメータ最適化の部分に，ニューラルネットワークを用いて効率化を図るという方法も提案されている^{（22）（23）}．これは，パラメータ最適化の際の目的関数が変数（パラメータ）の変化に対して極めて非線形性が強いとともに，その勾配がゼロに近いプラトー領域が非常に広いため，一般的な最適化アルゴリズム（遺伝的アルゴリズムも含む）による最適値探索がうまく機能しない場合が多く，その対応策として考案された方法である．このように，原子間ポテンシャル関数構築というスキームのどの部分に機械学習・深層学習的アプローチを導入すべきかという点についても，未だ議論が尽くされた状況ではなく，今後も様々なアイデアが提示され研究が進められていくと予想される．BartokやBehlerらが主張するように^{（2）（20）（24）}，「従来型原子間ポテンシャルと同等のコストで第一原理計算並みの精度と信頼性を持った」ポテンシャルが簡単に作成できるようになれば，原子モデルシミュレーションの適用範囲も飛躍的に広がるものと期待される．

〔梅野　宜崇　東京大学〕

目次に戻る

5.4　ディープラーニングによる外観検査

5.4.1　ディープラーニングによる外観検査の問題点

　近年，ディープラーニングによる画像認識は目覚ましい発展を遂げており，これらの成果は実利用の段階に入った．一方，工場などの生産現場では，古くから画像認識による外観検査が導入されているが，これらにディープラーニングを導入することで飛躍的な精度の向上を行った事例が報告されつつある．ディープラーニングを外観検査に導入するメリットは精度の向上だけにとどまらず，従来人手による特徴量，識別器の設計や細かなパラメータ設定を，データドリブンな学習に置き換えることによる導入時間の短縮や，一つの識別器による複数製品の検査，過去の事例から新しい製品への転移学習などによる汎用性の向上など，従来方法では得られない利点が期待されている．一方で，ディープラーニングを外観検査に応用する場合に，外観検査ゆえの問題がある．

　通常，製品の良品と不良品を判別する場合，2クラス（良品クラスと不良品クラス）を識別するニューラルネットワークを構築する．ニューラルネットワークを学習させるためには大量の良品サンプルと不良品サンプルが必要であるが，生産の現場において不良品は極稀にしか起こらないもので，大量の不良品サンプルを確保することは難しい．すなわち，入手可能なデータは，多くの場面で大量の良品サンプルと少量の不良品サンプルである．

　このような不良品サンプルが良品サンプルに比べ明らかに少ない状況では2クラス分類はうまく学習されない．ニューラルネットワークの学習は，通常識別結果の誤差（間違い）を最小にするようなネットワーク重みの最適化問題である．例えば，多量の良品サンプルが99.9%，少量の不良品サンプルが0.1%の割合で学習を行ったとする．この場合，いつも良品と答えるネットワークは99.9%の識別結果を得られるため最適化の必要がなく，不良を識別するようには学習されない．すなわち，強く偏りを持った学習データでは，ニューラルネットワークが適切な識別境界を学習することができない．また，良品は一定の水準以内の製品であるため画像としてのはらつきは小さいが，不良品には無限のパターンが存在するためばらつきが非常に大きい．このため，識別型のニューラルネットワークで仮に入手できた不良サンプルが識別できるように学習できたとしても，未知の不良品（学習に用いていない不良品）を不良品であると正確に識別できるとは限らない．

　そこで，近年では大量の良品サンプルからニューラルネットワークによって正常状態モデルを生成し，その正常状態を基として未知サンプルの異常度を算出する手法が用いられる．その代表的なモデルとして，AutoencoderやGenerative Adversarial Networks（GANs）による異常検知がある．

5.4.2　Autoencoderによる異常検知

　Autoencoder^（1）とは教師なしニューラルネットワークの一種で，図4-1のようなEncoder-Decoder構造を持っている．Encoderでは入力をエンコード（情報の圧縮）し，Decoderではエンコードされた情報からデコード（入力へ復元）する．Encoderによって得られた情報は入力をよく表す特徴となるため，特徴学習に用いられる．EncoderとDecoderの境界部分をボトルネックといい，この部分が低次元に圧縮された画像特徴である．外観検査に用いる際には，Convolution層，Deconvolution層をEncoderとDecoderに用いることで画像から空間的な構造を考慮した特徴を抽出することが多い．

図4-1　Coevolution Neural Network（CNN）を用いたAutoencoder構造

　Autoencoderを外観検査に用いる際には，大きく2種類のアプローチがある．1つ目は，Autoencoderが入力を復元するネットワークであることを用いた手法である．大量の良品サンプルのみを学習に用いたAutoencoderは，入力された未知の良品画像は適切に復元することができるよう学習される．一方，不良品サンプルは学習していないため，入力された未知の不良品画像の不良箇所は良品に復元されるか，もしくはでたらめな結果として復元される．すなわち，入力画像と出力画像の差分を取ることで不良箇所は値が大きくなる．そのため，入出力の差分値を異常度としてしきい値を設けることで正常と異常の識別を行うことができる．これは異物や大きな損傷といった不良に対して有効である（図4-2）．しかしこの場合，Autoencoderにより復元された不良箇所は本来「未定状態」といえる．すなわち，異常箇所は良品として復元されるか，出力結果がでたらめになるか未定である．もしくは，何も復元される入力画像のまま出力されるかもしれない．本手法にはそのような不安定さがある．

図4-2　Autoencoderの入出力画像の差分による異常検知

　2つ目は，Autoencoderが画像の特徴を学習可能であるという特性を活かした手法である．Autoencoderのボトルネックでは，学習された画像の特徴が得られる．大量の良品サンプルで学習することで抽出される特徴に対して，Gaussian Mixture Model（GMM）やOne-Class Support Vector Machine（OCSVM）といった従来の統計モデルに入力することで異常度を得る手法である．この手法は不良品であっても1つ目の手法で復元されてしまう場合に有効である．
　この2つの手法を併せ持つ手法として，Deep Autoencoding Gaussian Mixture Model（DAGMM）^（2）がある（図4-3）．DAGMMではCompression Network，Estimation Network，GMMの3つのモデルを持ち，Compression Networkで得られた特徴と差分値を入力変数とし，GMMによる異常検知をEnd-to-Endに行うモデルである．Estimation NetworkはGMMの負担率を算出する．これにより，得られた特徴と差分値を同時に考慮した異常検知を可能にしている．

図4-3　Deep Autoencoding Gaussian Mixture Modelのネットワーク構造

5.4.3　GANsによる異常検知

　GANs^（3）はGeneratorとDiscriminatorの2つのネットワークを持ち，Generatorはデータを生成し，DiscriminatorはGeneratorが生成したデータなのか本物のデータなのかを識別する（図4-4）．一部に，不良品サンプルが入手できないのでGANsを用いて不良品画像を生成させ，識別器の精度を向上させる試みも存在するが，それは間違いであることが多方面で指摘されている．

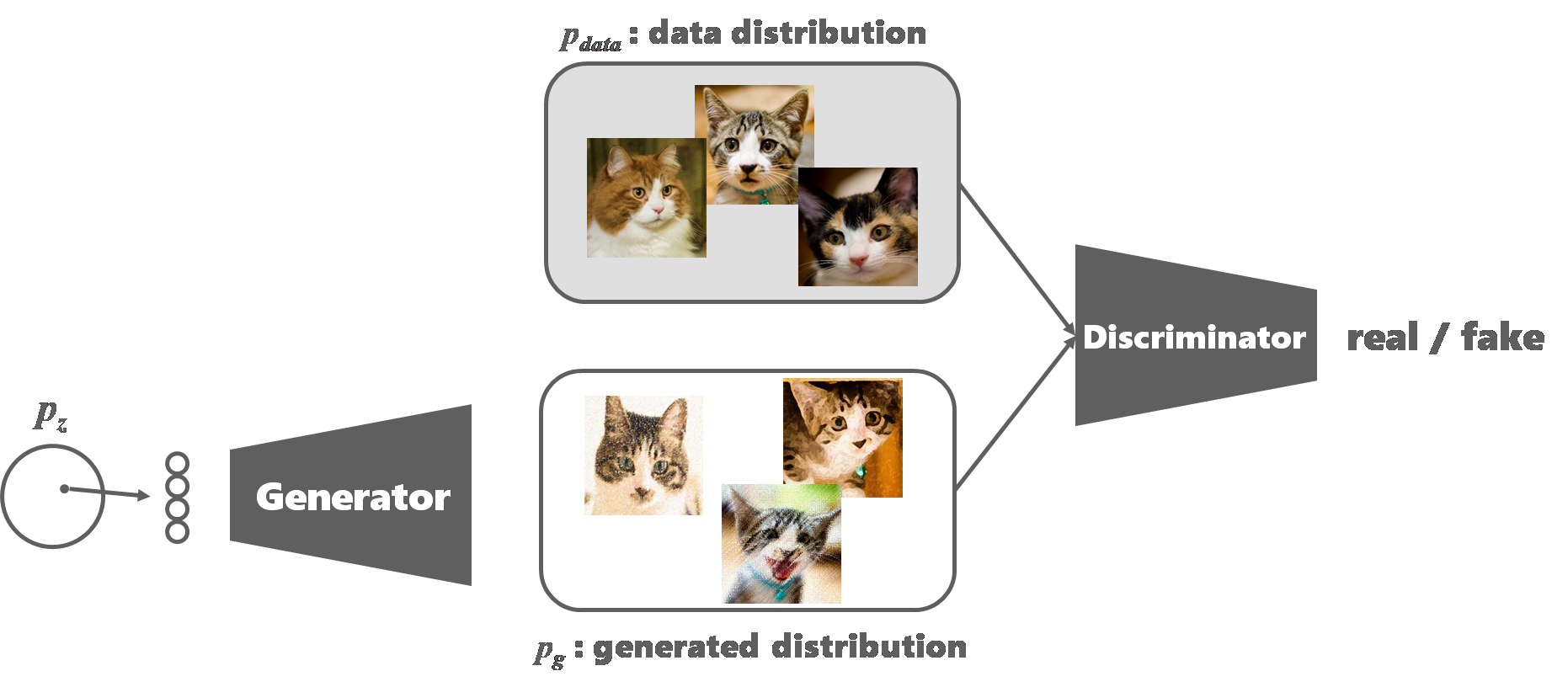
図4-4　基本的なGANsの枠組み

　そもそもGANsの学習には大量のデータが必要であるので不良品サンプルが必要なことに変わりがないことに加えて，GANsはそのデータの分布を捉え生成するモデルであるため，まだ見ぬ不良データを生成することはできないからである．また，一般画像認識においてGANsで生成された画像を用いてデータセットを水増しすると認識精度が下がることがECCV2018にて報告されている^（4）．そのため，GANsを用いた異常検知では不良品を生成するのではなく，正常モデルを生成するためにGANsを用いるモデルが近年提案されている．

　Efficient GAN^（5）は従来手法であるAnoGAN^（6）やADGAN^（7）を改良したモデルであり，BiGANと呼ばれる生成と特徴抽出を同時に学習するGANを用いて，再構成されたデータとデータから抽出された特徴から異常度を算出している（図4-5）．これは前述のDAGMMに非常に近いアイデアである．

図4-5　Efficient GANのネットワーク構造

　またGANsのDiscriminatorは本物のデータ（real）と生成されたデータ（fake）を識別するため，本物＝正常データとすればDiscriminatorが異常検知器になるのではないかというアプローチもいくつか存在するが，これも間違いであることが報告されている．GANsにおけるDiscriminatorはデータ分布と生成分布がどれだけ離れているかを算出するモデルであり，異常品の情報は一切獲得していない．すなわちまだ見ぬ異常を検知することは不可能である．そもそも，Generatorはrealに近いデータ（fake）を生成し，Discriminatorはそのrealとfakeを識別するモデルとなるため，最終的にはDiscriminatorによる識別境界はrealとそれ以外を分けるものとはならない．しかし，GANsの構造に工夫を加えることでDiscriminatorを異常検知器として用いる方法が提案されている．

　Complementary GANは，図4-6に示すように目的関数を工夫し生成分布を正常データの補集合分布に近づける学習をさせることで，Discriminatorは正常とそれ以外が識別できるようになり異常検知が行えるというモデルである^（8）．

図4-6　Complementary GANによる正常と異常の識別

5.4.4　適用事例

　乾燥麺の良品サンプルに対してAutoencoderを学習し，入出力の差分による異常検知を行った事例を示す．この事例では正常の乾燥麺の画像のみからAutoencoderを学習し，図4-7に示すように正常には無いような焦げた麺の破片が混入した箇所を不良としている．焦げた麺の破片領域に大きな差分値が現れていることがわかる^（9）．

図4-7　Autoencoderの入出力画像の差分による異常検知例

　次に，AutoencoderとGANsの枠組みを合わせたAdversarial Autoencoder（AAE）^（10）を用いた事例を示す．AAEはAutoencoderとDiscriminatorから構成され，Autoencoderのボトルネックで得られる特徴量の分布を任意の分布に従わせることができるGANsの一手法である．その分布を標準正規分布とし，抽出された特徴にHotelling’s T-Squaredを適用することで，AAEの学習を行うだけで未知データの異常度が算出可能である^（11）．図4-8は白米の異常検知にAAEを適用した事例である．白米データセットは，訓練用データが29,194枚，テスト用データが8,739枚から構成され，データセットの中には，傷や欠け，白濁を含むような異常データが含まれる．なお，データの異常率は6.5%ほどで，今回はこれら良品，不良品を区別せず学習させる教師なし学習で行っている．

図4-8　Adversarial Autoencoderによる異常検知例

〔加藤　邦人　岐阜大学〕

目次に戻る

5.5　ペリダイナミクス

5.5.1　はじめに

　破壊は構造体の信頼性を左右する重要な現象であるにも関わらず，そのシミュレーションは容易でない．有限要素法において破壊を模擬するためには，ある条件下で要素を消去する，Cohesive要素，Extended FEM等の手法によりき裂近傍における物理量不連続の問題を回避する，といった方策を用いる必要があるが，過度に細かいメッシュを要する，任意の場所で生じる破壊を再現できない，同時に進行する多数のき裂進展，相互作用の解析が容易でない，等の問題が存在する．そもそも，有限要素法がその定式を依拠する局所弾性論では，き裂先端等の応力特異点を陽に含んだ解析を実施することが難しい．破壊解析を実施するためには，応力特異点を生じうる幾何構造をその系に含んだとしても計算が発散しない理論をそのベースとすることが望ましいと言える．

　ペリダイナミクスは，米国サンディア国立研究所のSillingによって提案された粒子法ベースの連続体変形解析手法である^（1）．積分形式による定式であること，ある程度大きい影響半径（ホライゾンと呼ばれる）内に位置する近傍粒子の情報を利用すること，粒子間結合の破断によって破壊を表現すること，をその特徴としている^（2）．”周囲の”という意味を持つ接頭辞”peri”をその名に冠することから理解できるように，ある程度広い周囲の情報を取り込んだ上で連続体の運動を模擬することがその最大の特徴である．そういう意味では，ペリダイナミクスは分子動力学法やQuasicontinuum法といった原子ベースの解析法に近い：ある程度遠方まで及ぶ粒子間モデルポテンシャルを連続体の変形を模擬できるように構築した粒子動力学手法がペリダイナミクスである．非局所的に情報を取りこむことから，局所弾性論において見られるような，応力特異点等の物理量不連続の問題が生じない．このことが，ペリダイナミクスが破壊に適した計算法と見做される理由である．本稿ではペリダイナミクスの定式を概観し，その課題と応用について紹介する．

5.5.2　ペリダイナミクスの3つの定式

　ペリダイナミクスには，Bond-based, Ordinary State-Based（OSB）, Non-Ordinary State-Based（NOSB）の3つの定式が存在する^（2）．これらの定式の差異を簡潔に示したものを図5-1に示した．ある粒子に生じる力は，その粒子を中心とするある影響半径，ホライゾンの中に位置する粒子群からの相互作用の和として定まる．粒子jがある粒子iに作用して力F_jiが生じるとき，そこには同様にF_ijが生じる．Bond-based定式では，このF_ji，F_ijが同じ線上に存在し，かつ，その大きさは等しい．Ordinary State-Based定式では，これらの2体間力は同じ線上に存在するが，大きさは異なっていてもよい．Non-Ordinary State-Based定式では，必ずしも2体間力は同一線上にある必要はなく，大きさも等しい必要はない．従って，OSB，NOSBの定式はBond-basedの定式から少しずつ制限を緩めたものとして解釈できる．

図5-1　ペリダイナミクス粒子における2体間力：
（a）Bond-based定式，（b）OSB定式，（c）NOSB定式

　Bond-Based定式は最も基礎的なペリダイナミクスの定式である^（1）．変形下にある粒子の変位を変数としてひずみエネルギーを定義し，その粒子位置の微分として粒子に生じる力を求めることで，動力学シミュレーションを実施できる．破壊基準としては，結合長さがある一定量を超えたときに切断する臨界結合伸びが用いられることが多い．Bond-based定式の欠点は，その基本的な定式において，線形弾性体のみしか扱えない，ポアソン比が0.25に固定される，ということである．OSB定式はこれらの問題を解決するために，Bond-Based定式を上述の通り拡張したものである^{（5）（6）}．この拡張により，任意のポアソン比を設定することが可能となり，材料非線形の取扱いが可能となった．現在では，延性材料^（6），複合材料^（7）の材料構成則を構築した研究例がある．また，理論的側面としては，文献（8）においてOSBモデルの客観性が議論されている．

　Bond-based定式，OSB定式における1つの問題は，局所弾性論に立脚しないことから，応力とひずみという連続体力学の概念，また，それらの関係を記述する材料構成則がその基本的な定式の中に存在しないことである．従って，それらの定式においては，目標とする材料の振る舞いを模擬するように，変位をパラメータとして有る種のモデルポテンシャルを構築する必要がある．一方で，NOSB定式は従来の連続体力学に依拠した定式を持っており，これらの問題を回避することができる^（4）．そこでは，変形勾配テンソルを粒子の変位から推定し，ひずみテンソルを求め，構成則を通じて応力，粒子に生じる力を評価する．最初に提案されたNOSB定式はTotal Lagrange法に基づくものであったが，近年ではUpdated Lagrange法に基づくものも提案されている^（9）．その利点は，これまでに有限要素法の関連研究の中で蓄積されてきた構成則という財産をそのまま転用できるところにある．実際に，粘塑性材料へ適用した研究が存在する^（10）．また，個々の粒子間結合上で定義されたエネルギーを破壊基準とする手法も提案されており^（11），それを線形破壊力学のパラメータであるエネルギー解放率へ接続することに成功している．その一方で，NOSBの定式は従来の連続体力学に基づくことから，その非局所弾性論としての性質には若干の疑義が残る．実際に，き裂近傍の解析ではその数値安定性が問題となっており^（6），そこでの妥当性，精度についてはより詳細な議論が必要であるように思われる．

5.5.3　課題と応用例

　定式の如何に関わらず，ペリダイナミクスシミュレーションにおいて生じる大きな障害の１つが計算量の問題である．影響半径としてのホライゾンを大きくとった場合には，多くの粒子と相互作用することになるため計算量が増大する．また，有限要素法に比して離散化性能が低いために，有限要素法と同程度の精度を得るためには多くの粒子数を要する．この計算量の問題を克服する目的で種々のアプローチが試みられており，粒子の粗密度を変更する手法^{（12）（13）}，有限要素法と接続する手法^{（14）（15）}，大規模並列計算機^{（16）（17）}を用いる手法，陽解法において複数のタイムステップを用いる手法^（18）等様々なものが提案されている．計算量の問題により各種の破壊実験との定量的な比較が難しい現状は問題として指摘されており^（19），直近に解決されるべき問題として研究が進められている．

　現状において未成熟であり様々な問題を有するペリダイナミクスであるが，破壊シミュレーションへの適性が注目された結果，ここ十年ほどの間で多くの応用研究がなされた．き裂の進展や分岐のシミュレーション^{（20）-（22）}，衝撃により生じる破壊のシミュレーション問題^{（14）（23）}のみに留まらず，多結晶体等の微視的問題^（24）やマルチフィジックス^{（25）（26）}への応用も広がっており，理論・応用の両面で更なる発展が期待される．

〔椎原　良典　豊田工業大学〕

目次に戻る