1．　はじめに

本稿では，閉じた系と開いた系に対する熱力学第一法則の具体的な表現を学ぶとともに，状態量と状態量でないもの，開いた系で定義されるエンタルピーについて理解する。

2．　閉じた系の第一法則

ここでは，閉じた系の熱力学第一法則の具体的な表現の方法を学ぶ。図3.1に示した，気体が封入されたシリンダとピストンの系を考える。シリンダとピストンに囲まれた気体部分が系となる。この際，シリンダから気体が流出することも，外部から気体が流入することもない。このように，系に対して物質の流入出がない系を，閉じた系という。一方，系に対して物質の出入りが存在するような系のことを，開いた系という。

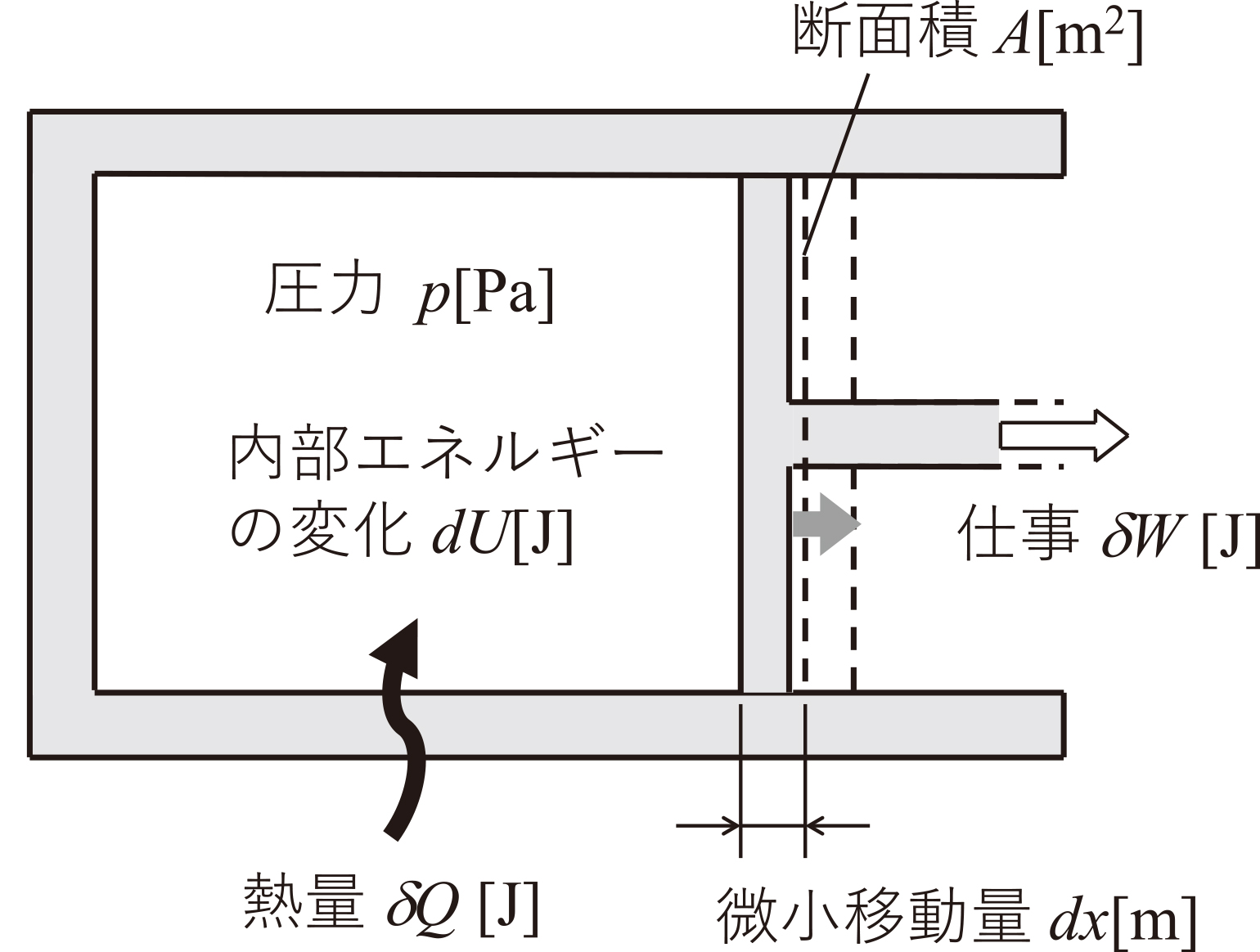
図3.1　閉じた系

この閉じた系に対して，外部から微小熱量$\delta Q$[J]を供給し，気体の内部エネルギーの微小変化量$dU$[J]，さらに準静的過程のもとに，ピストンが$dx$[m]だけ移動した際の気体が外部に対してした微小な仕事$\delta W$[J]から，熱力学第一法則の具体的な表現は，

\[\delta Q = dU + \delta W = dU + pAdx = dU + pdV\]

(1)

のように書ける。式が表すとおり，外部から系に供給された熱量のうち，一部が系の内部エネルギーの変化に充てられ，それ以外は系が外部に対してした仕事となる。ここで，$pdV$で表現される，系が外部に対してした仕事のことを絶対仕事という。外部から作用する力と系の気体が膨張する際の圧力が釣り合いながらピストンは移動するため，式(1)で示される関係は，準静的過程のもとに成立するものであることに注意する。

3．　状態量

系が，外部からの力と釣り合い，周囲の温度と等しく，温度や圧力などの物理量が時間的に変化しない状態のことを熱力学的平衡状態という。ある系が熱力学的平衡状態にあるとき，その系の状態は，その状態で定義される物理量を用いて表現することができる。例えば，ある系が熱力学的平衡状態にあるとき，その温度が$T_1$であるとする。その状態が変化し，温度$T_2$の熱力学的平衡状態になるとき，変化の過程に依存せずに，温度は$T_2$と表現される。圧力や体積も同様に表現でき，このような物理量のことを状態量という。状態量には，温度，圧力，体積のほか，内部エネルギー，エンタルピー，エントロピーなどがある。状態量のうち，温度，圧力のように，物質の質量に依存せずに決定する状態量を示強性状態量，体積，内部エネルギーなどのように質量によってその量が変化する状態量のことを示量性状態量という。示量性状態量の場合には，その状態量を単位質量あたりで表現することがあり，その場合にはそれぞれの状態量の前に「比」をつけて表現する。例えば，単位質量あたりの内部エネルギーのことを比内部エネルギー，単位質量あたりの体積のことを比体積という。

一方，状態が変化する過程に依存して決定される物理量が絶対仕事と熱量であり，これらは状態量ではない。本稿では，式(1)のように，状態量である内部エネルギーの微小変化は$dU$と表現し，状態量ではない微小な熱量および微小な絶対仕事を$\delta Q$および$\delta W$と表現する。

先にも述べたとおり，状態量は変化の過程に依存せず，その変化量は最初の状態と最後の状態のみで決定する。そのため，状態1から状態2までの内部エネルギーの変化量を考える場合，

\[\Delta U = \int_1^2 dU = U_2 – U_1\]

(2)

のように表現できる。これより，微小変化の釣り合いを考えた式(1)をある状態1から状態2への変化を考える際には，

\[Q_{12} = \int_1^2 dU + \int_1^2 pdV = U_2 – U_1 + \int_1^2 pdV\]

(3)

となる。ここで，$Q_{12}$は，状態1から状態2の過程で系に供給された熱量を表す。この式より，絶対仕事が変化の過程に依存して決定されるために，熱量も同様に変化の過程に依存する物理量となり，状態量ではないことがわかる。

式(1)を，系を構成する物質の単位質量あたりの量を使って表現する場合，

\[q_{12} = \int_1^2 du + \int_1^2 pdv = u_2 – u_1 + \int_1^2 pdv\]

(4)

のように，本稿では各記号の小文字で表現することとする。

4．　開いた系の第一法則

先にも述べたとおり，系に物質の流入出がある系を開いた系という。ここでは，開いた系における第一法則を学ぶ。図3.2に示すような仕組みを考える。入口から作動流体が流入し，熱量を受け取り，外部に仕事をしたのち，出口から流出する。ここでは，これらの動作が連続して行われ，一定の熱量を連続して供給し，一定の仕事を連続して取り出すような系を考える。このような系では，系内の質量が保存する必要があるため，入口と出口での質量流量は等しい。また，系内の温度や圧力は，時間的に変化しないものとすると，このような系を定常流動系という。

図3.2　開いた系

この系において，入口では内部エネルギー$U_1$の流体が，圧力$p_1$，体積$V_1$（$=A_1 \mathit{\Delta} x_1$）で流入すると，入口で流入することにより系が仕事を受ける。このような仕事を流動仕事といい，

\[W_{f1} = p_1 A_1 \Delta x_1 = p_1 V_1\]

(5)

と表せる。流動仕事は，入口にピストンがついていて，ピストンを押し込むことの仕事と考えると理解しやすい。系に流入する流体の内部エネルギーと流入する流体が系にした仕事の和が系内に流入する。すなわち，入口では，

\[H_1 = U_1 + W_{f1} = U_1 + p_1 V_1\]

(6)

のエネルギーが流入する。同様に，出口では，内部エネルギーが$U_2$となった流体が，圧力$p_2$と体積$V_2$で流出する際に外部に仕事をする。出入口の高さの変化による位置エネルギーと流体の速度による運動エネルギーは無視できるとすると，系内の温度は時間的に変化せず，内部エネルギーの変化がないことから，この系での第一法則は，

\[Q_{12} = H_2 – H_1 + W_t = (U_2 + p_2 V_2) – (U_1 + p_1 V_1) + W_t\]

(7)

と書ける。ここで，$H$（$=U+pV$）で表される物理量は，流動仕事を含んだ開いた系に対するエネルギーを表している。これをエンタルピーと定義する。エンタルピーの単位は[J]であり，内部エネルギー，圧力，体積がいずれも状態量であることから，エンタルピーも状態量の一つであり，開いた系に限らず，閉じた系，液体や固体に対しても$U+pV$で定義される量である。

ここで，第一法則の表現として，それぞれの系に対して式(3)と式(7)が示された。しかし，いずれの式も，表現の仕方は異なるものの，本質的には同じエネルギーの保存を表したものであり，閉じた系にも開いた系に適用できる点に注意が必要である。式(3)と式(7)を比較すると，開いた系における絶対仕事は，$W_t+(p_2 V_2-p_1 V_1)$に相当する。流動仕事は，流体の系への流入出に伴う仕事であり，外部に取り出せる仕事は$W_t$[J]のみとなる。この仕事$W_t$のことを，工業仕事という。すなわち，開いた系に対する第一法則では，系に供給した熱量は，系から外部に取り出した工業仕事$W_t$と系の出入口での作動流体のエンタルピーの変化と釣り合うこととなる。

演習問題3.1：第一法則の利用

$U=CT$の関係で内部エネルギーが温度に比例する気体が，状態1（$p_1$[Pa]，$V_1$[m³]，$T_1$[K]）から状態2（$0.5p_1$[Pa]，$3V_1$[m³]，$T_2$[K]）まで$p$-$V$線図上を直線的に膨張した。この過程で気体が受けた熱量を求めよ。

（答：$\displaystyle \boldsymbol{C(T_2 – T_1) + \frac{3}{2} p_1 V_1}$）

---

＜正員＞

熊野 寛之

◎青山学院大学　理工学部機械創造工学科　教授

◎専門：伝熱工学，固液相変化伝熱，相変化スラリー，ハイドレート，物性値計測