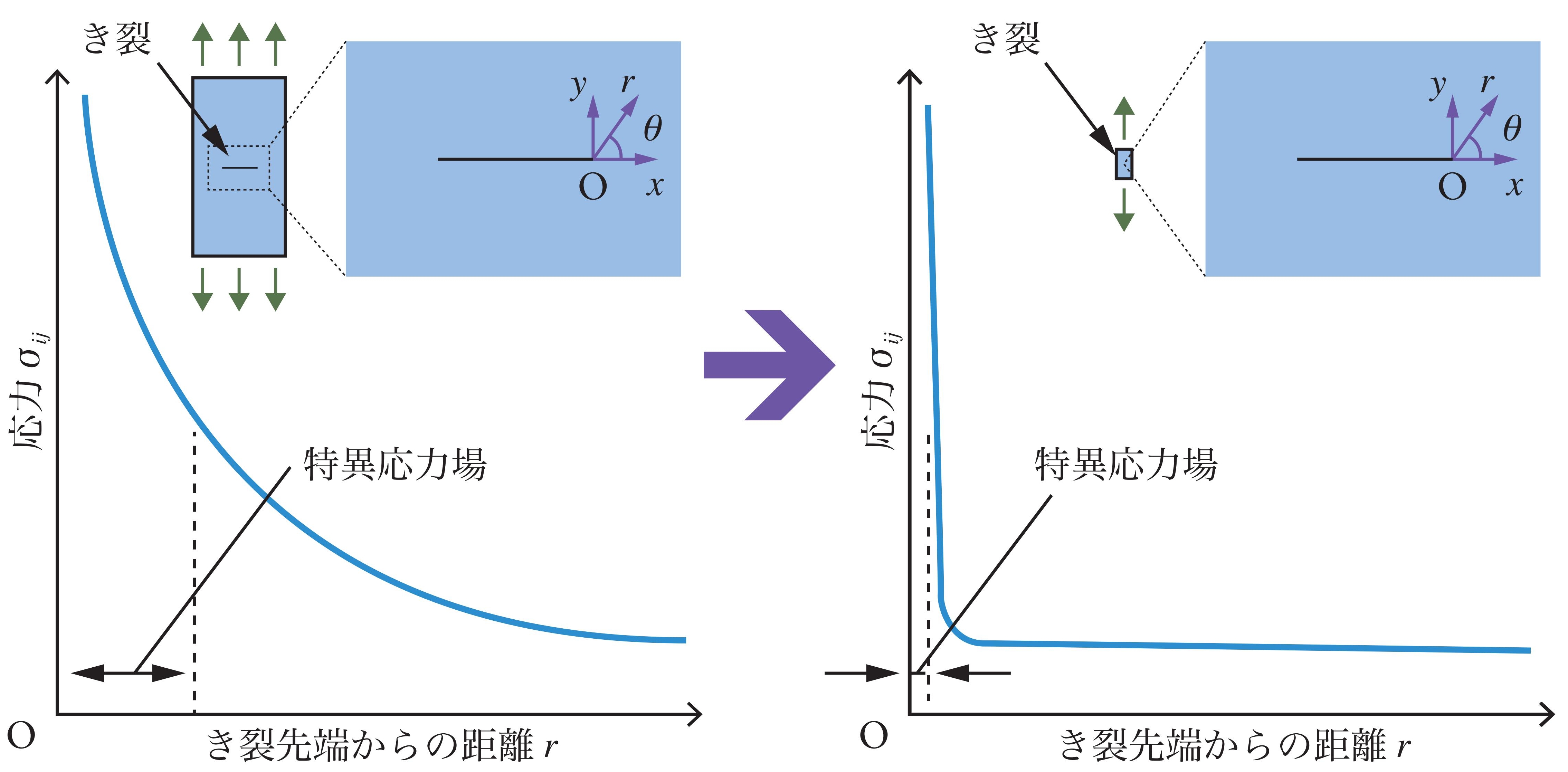
図1　き裂先端における特異応力場領域の寸法依存性

“ 欠陥をあやつる”- 破壊力学 –

破壊を支配する欠陥の力学

歴史上記録に残っている最も古い材料強度試験はレオナルド・ダ・ヴィンチが行った試験であり、鉄線が長くなるほど耐えられる強さ（強度）が低下するというものであった。しかし、現代の技術で作製される鉄線の強度は、太さが同一であれば長さに依存することはない。ダ・ヴィンチの結果は、彼が用いた鉄線中に欠陥が存在し、欠陥が全体の強度を支配したことを暗に示している。欠陥が強度を支配する場合、材料の長さ（体積）が増大すると致命的な欠陥を内包する確率が高くなり、材料強度は低下する。このように材料は、欠陥の存在によって時として期待したよりも低い力で予期しない破壊を起こすことがある。このため、欠陥を考慮に入れた定量的な強度評価手法が必要とされた。

破壊強度と欠陥（き裂）寸法との定量的な関係は、1920年にGriffith^（1）によって示され、彼は、き裂成長によるひずみエネルギーの増分が材料の表面エネルギーより充分大きければ、欠陥は不安定的に破壊することを述べた。さらに1957 年にIrwin^（2）は、き裂先端近傍の応力は、ある係数を用いて表示できることを示した。線形弾性均質体中のき裂に開口モード（モードI）の負荷が加わった場合、き裂先端に直角座標（x、y、z）あるいは円柱座標（r、θ、z）を配置すると、き裂先端近傍における応力成分σij （i、j = x, y, z）は近似的に以下の式で表すことができる。

ここで、r はき裂先端からの距離、K_I は応力拡大係数と呼ばれる定数、f_ij（θ）はθ の無次元関数である。式（1）に示されるように、き裂先端近傍の応力は √rに反比例した分布となり、き裂の先端（r = 0）では無限大に発散する（特異応力場）。このため、最危険点であるき裂先端一点の応力値を駆動力として、き裂を有する材料の強度を普遍的に定量化することができない。破壊力学（線形破壊力学）は、き裂先端近傍における特異応力場の場の強さである応力拡大係数K_I に着目し、欠陥を有する材料の破壊現象を定量的に取り扱う工学手法である。近代産業の著しい発展は、人類が「欠陥をあやつる」破壊力学を手に入れたことが最大の要因と言っても過言ではない。

一方、近年では、スマートフォンや各種微小センサ等、無数のナノ・マイクロ材料で構成されたデバイスが世の中に溢れ、我々の生活を便利かつ豊かなものにしている。これら近代エレクトロニクス産業は、先人の膨大な努力により成熟に向かっていた破壊力学に対して、ナノスケール破壊／界面破壊という新たな研究分野を生み出した。